다른 글에서 수학 문제 풀이에 유용한 울프럼 알파를 이용하여 적립식 누적 수익률을 거치식 연복리 수익률로 환산하는 방법을 살펴보았습니다. 5년간 연 단위로 적립식으로 투자해서 30% 수익률을 얻었다면, 대략 거치식 연 8.9% 복리 수익률에 해당했습니다. 관련 글: 적립식 수익률을 거치식 수익률로 환산해서 비교하기 (울프럼 알파 vs 챗GPT + 제미나이 + 코파일럿)
이 글에서는 파이썬을 이용하여 거치식과 적립식의 수익률을 그래프로 그려보고, 서로 변환할 수 있는 추정 방법을 만들어 봅니다.

누적 수익률(자산비) 모델링
먼저 거치식 누적 수익률을 모델링해 보겠습니다. 복리 계산의 편의를 위해 자산비를 사용합니다. 자산비는 수익률 + 1입니다.
단위 기간에 r씩 성장한다면, k회 복리 투자하면 자산은 (1 + r)ᵏ배가 됩니다. 예를 들어 연 10%씩 성장한다면, 1년 투자하면 1 + 10% = 1.1배, 2년 투자하면 (1 + 10%)² = 1.21배가 됩니다.
적립식은 각각의 투자금을 거치식으로 투자한다고 생각하면 됩니다. 첫 투자금은 거치식과 마찬가지로 (1 + r)ᵏ배가 될 것입니다. 두 번째 투자금은 투자 단위 기간의 수가 1회 적기에 (1 + r)ᵏ⁻¹배가 됩니다. 가장 최근 투자금은 1회 단위 기간을 지났으니 (1 + r)배가 될 것입니다. 정리하면 다음과 같은 수식이 됩니다.
(1 + r)ᵏ + (1 + r)ᵏ⁻¹ + ... + (1 + r)² + (1 + r)
전체 투자금을 1 / k로 나누어서 투자했으니, 위의 결과를 k로 나누어주면 됩니다.
파이썬으로 이를 구현해서 그래프로 그려봅니다.
r = 0.1
lumpsum_l = []
dca_l = []
my_range = range(1, 20 + 1)
for k in my_range:
lumpsum = (1 + r) ** k
dca = ((1 + r) ** np.arange(1, k + 1)).mean()
lumpsum_l.append(lumpsum)
dca_l.append(dca)
df = pd.DataFrame([lumpsum_l, dca_l]).T
df.columns = ['거치식', '적립식']
df.index = my_range
df.plot()
plt.yscale('log')
plt.xticks(my_range[::-2])
yticks = np.array([0, 0.5, 1, 2, 3, 4, 5, 6])
plt.yticks(yticks + 1, [f'{x * 100:.0f}%' for x in yticks])
plt.xlabel('투자 기간 (년)')
plt.ylabel('누적 수익률')
plt.show()주요 부분을 살펴봅니다.
r = 0.1거치식의 연평균 성장률을 10%로 설정했습니다.
lumpsum_l = []
dca_l = []
my_range = range(1, 20 + 1)거치식 자산비를 담을 변수로 lumpsum_l, 적립식 자산비를 담을 변수로 dca_l을 준비했습니다. my_range에는 1부터 20까지 1씩 증가시킨 목록을 지정했습니다. 파이썬에서 대부분의 범위는 마지막값 직전까지이니 range(1, 20 + 1) = [1, 2, 2..., 20]이 됩니다. 이후에 이 범위를 재사용하기 위해 변수로 설정했습니다.
for k in my_range:
lumpsum = (1 + r) ** k
dca = ((1 + r) ** np.arange(1, k + 1)).mean()
lumpsum_l.append(lumpsum)
dca_l.append(dca)앞에서 소개한 방식으로 거치식 자산비 (1 + r)ᵏ를 계산했습니다. ** 연산은 지수승을 의미합니다. 적립식은 1부터 k까지 숫자를 만들어서 (1 + r)에 각각 지수승을 한 후 평균을 내면 됩니다.
적립식 자산비는 배열 연산(array operation)을 사용했습니다. 배열 연산은 익숙해지면 간결하면서 이해하기 쉬운 1줄의 코드로 여러 줄을 코드를 대체할 수 있습니다. 공부해 두면 편리합니다. 구글 시트나 마이크로소프트 엑셀의 경우에도 배열 연산을 지원하니 관심 있으신 분은 살펴보시기 바랍니다.
df = pd.DataFrame([lumpsum_l, dca_l]).T
df.columns = ['거치식', '적립식']
df.index = my_rangeDataFrame을 만들고, 칼럼명을 붙였습니다. 색인은 연 단위 투자 기간으로 앞에서 정의한 my_range를 재사용했습니다.
plt.xticks(my_range[::-2])x축 눈금을 my_range로 설정했습니다. 파이썬에서 범위를 지정하는 방법은 [start_index : end_index : step]입니다. step을 -2로 두었기에, 끝에서부터 2씩 감소시키라는 의미가 됩니다. [20, 18, ..., 2]가 만들어집니다. 눈금은 순서에 상관없기에 그래프 좌우가 바뀌지 않습니다.
결과는 다음 그래프와 같습니다.

파란색의 거치식 누적 자산비는 로그 스케일에서 직선으로 나타납니다. 의외로 오렌지색의 적립식 누적 자산비로 로그 스케일에서 직선처럼 보입니다.
연평균 성장률
적립식 누적 자산비가 로그 스케일에서 선형인지 연평균 성장률로 환산해서 다시 그려봅니다.
(df.pow(1 / df.index, axis = 0) - 1).plot()
plt.gca().yaxis.set_major_formatter(PercentFormatter(xmax = 1, decimals = 0))
plt.xticks(my_range[::-2])
plt.xlabel('투자 기간 (년)')
plt.ylabel('연평균 성장률')
plt.show()
df의 색인 df.index에는 투자 년수가 들어있습니다. 이를 이용하여 기하 평균을 계산하면 연평균 자산비가 됩니다. 여기에서 1을 뺀 연평균 성장률을 만들어 그래프로 그렸습니다.

투자 기간이 1년인 경우에는 거치식과 적립식의 자산비는 모두 (1 + r)로 동일하기에 연평균 성장률은 둘 다 10%입니다. 투자 기간이 점차 늘어나면 거치식은 연평균 수익률이 유지되지만, 적립식의 연평균 수익률은 낮아집니다. 새로 적립한 금액은 투자로 인해 증가하지 않은 원금이기 때문입니다.
어느 정도 투자 기간이 경과되면, 지금까지 투자한 금액이 새로 투자하는 금액보다 훨씬 커지게 됩니다. 예를 들어 매년 100만원씩 5년간 투자했다면, 500만원은 이미 투자되어 불어난 상태이고, 신규로 투자하는 100만원은 기존 투자 원금의 20%입니다. 기존 투자금은 지난 5년간의 투자로 인해 늘어난 상태이기에, 금액으로 보면 신규 투자금은 기존 자산의 20% 이하가 됩니다.
대략 20년까지 보면, 거치식의 연평균 성장률이 10%일 때, 적립식은 6% 정도를 유지하고 있습니다. 이 때문에 로그 스케일에서 직선처럼 보였던 것입니다.
거치식의 연평균 성장률이 5%인 경우와 15%인 경우도 그려 비교해 봅니다. y축 상대 범위를 동일하게 지정하기 위해 plt.ylim(r * 0.5, r * 1.01)로 설정했습니다.



엇비슷한 형태입니다. 대략 5 ~ 20년 사이에서 적립식은 거치식 연평균 수익률의 60% 정도를 보여주고 있습니다.
투자 기간을 40년까지 늘려 그리면 다음과 같습니다.
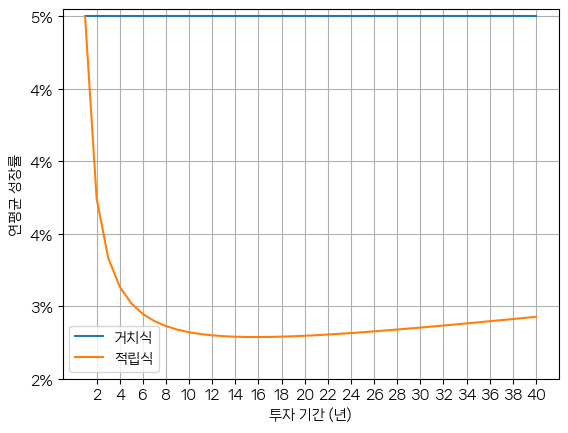


40년으로 투자 기간을 늘려도 거치식 연평균 성장률의 60% 수준에서 크게 벗어나지 않는 것을 알 수 있습니다.
거치식과 적립식 수익률의 근사 추정
연평균 성장률이 10% 내외인 자산에 대해 5 ~ 30년 정도의 투자 기간이라면, 적립식의 연평균 성장률은 거치식의 60%로 근사하여 추정할 수 있습니다.
예를 들어 연평균 성장률 12%를 기대할 수 있는 어떤 자산에 20년간 투자한다면, 적립식으로는 대략 12% × 60% = 7.2% 정도의 연평균 적립식 수익률을 예상할 수 있습니다. (1 + 7.2%)²⁰ - 1 ≒ 300%이니, 20년 후 자산이 투자금 대비 4배 정도로 불어날 거라 추정할 수 있습니다.
적립식으로 7년간 투자해서 100% 수익률을 얻었다면, 적립식 연평균 성장률은 (1 + 100%)¹ᐟ⁷ - 1 ≒ 10.4%입니다. 거치식으로 환산하면 10.4% / 60% ≒ 17.3%에 해당됩니다. 7년간 100% 적립식 수익률은 거치식으로 보면, 상당히 높은 수익률이라 볼 수 있습니다.
정리하며
대개의 개인 투자자는 장기 적립식으로 투자합니다. 처음부터 거치식으로 투자할 목돈을 가지고 있지 않기 때문입니다. 거치식 수익률 그래프를 보면 장기 투자를 통해 큰 자금으로 불릴 수 있을 듯 하지만, 적립식의 연평균 성장률은 거치식의 60% 정도이기에, 복리 효과에 의해 이보다 훨씬 낮은 장기 수익률을 얻게 됩니다.
거치식 및 적립식 연평균 성장률에 인플레이션을 고려하면, 정액(동일 금액) 적립식은 동일 가치 적립식으로 바뀌게 됩니다. 매 투자마다 동일한 가치를 가지도록 투자금을 증액시켜 가며 투자하는 경우가 됩니다.
그래프로 보여준 장기 15% 실질 성장률은 달성하기 쉽지 않습니다. 인플레이션까지 고려하면, 대략 7 ~ 10% 정도의 거치식 실질 장기 연평균 성장률이 현실적입니다. 이는 4.2 ~ 6% 정도의 적립식 실질 장기 연평균 성장에 해당합니다. 이 때문에 일반적인 개인 투자자는 절약과 근로 또는 사업 소득 증대에도 신경을 써는 것이 바람직합니다.
인플레이션을 고려한, 거치식, 적립식, 인출식 투자를 시뮬레이션하는 방법에 대한 설명과 ETF를 이용한 구체적인 사례는 <구글 시트로 시작하는 투자 포트폴리오 분석 - 오렌지사과의 불친절한 워크북>이나 <파이썬으로 그려보는 투자 포트폴리오 분석 - 정량적 투자 분석을 위한 입문서>를 참고하기 바랍니다.
책 출간 안내: 내부수익률 - 당신의 실질 투자수익률 (적립식 투자자와 은퇴자를 위한 현금 흐름을 고려한 수익률 계산법) 출간에 부쳐 (샘플북 포함)
참고 서적:
이어지는 글: 파이썬을 이용한 수치 해석 (적립식 수익률에 해당하는 거치식 성장률을 찾아보자) [파이썬 분석 부록 A3]
관련 연재: 순서대로 읽으시길 권합니다.
- 적립식 수익률을 거치식 수익률로 환산해서 비교하기 (울프럼 알파 vs 챗GPT + 제미나이 + 코파일럿)
- 거치식과 적립식 수익률을 서로 환산해 보자 (어떻게 추정하면 적절할까?) [파이썬 분석 부록 A2] (본 글)
- 파이썬을 이용한 수치 해석 (적립식 수익률에 해당하는 거치식 성장률을 찾아보자) [파이썬 분석 부록 A3]
- 임의 적립식 투자 수익률에 해당하는 거치식 성장률을 찾아보자 [파이썬 분석 부록 A4]
- 구글 시트로 임의 적립식 투자 수익률에 해당하는 거치식 CAGR을 구해보자 [데이터 분석 부록 C1] (골 시크 Goal Seek)
- 엑셀로 임의 적립식 투자 수익률에 해당하는 거치식 CAGR을 구해보자 [데이터 분석 부록 C2] (목표값 찾기)
연재 목록: 자산 배분 분석 방법 책 소개, 연재글 및 사례 모음 [목록]
함께 읽으면 좋은 글 (최신 글)
- 적립식 수익률을 거치식 수익률로 환산해서 비교하기 (울프럼 알파 vs 챗GPT + 제미나이 + 코파일럿)
- [중급 24] 베이즈 정리와 추론 - 나주사씨의 친구들은 주사위를 어떻게 추정했을까? (고정된 수익률 분포를 완벽하게 아는 경우)
- [중급 23] 숨겨진 주사위는 몇 면일까? (모집단의 추정)
- [중급 22] 투자 정보의 가치는 얼마일까? (누군가 내일의 주가 수익률을 알려준다면 초모험씨는 얼마나 지불할 수 있을까?)
- [중급 21] 섀넌의 도깨비(Shannon's Demon) - 현실에서는 왜 찾기 어려울까?
함께 읽으면 좋은 글 (인기 글)
'주식투자' 카테고리의 다른 글
| 엑셀로 임의 적립식 투자 수익률에 해당하는 거치식 CAGR을 구해보자 [데이터 분석 부록 C2] (목표값 찾기) (0) | 2025.05.29 |
|---|---|
| 구글 시트로 임의 적립식 투자 수익률에 해당하는 거치식 CAGR을 구해보자 [데이터 분석 부록 C1] (골 시크 Goal Seek) (2) | 2025.05.28 |
| 임의 적립식 투자 수익률에 해당하는 거치식 성장률을 찾아보자 [파이썬 분석 부록 A4] (1) | 2025.05.28 |
| 파이썬을 이용한 수치 해석 (적립식 수익률에 해당하는 거치식 성장률을 찾아보자) [파이썬 분석 부록 A3] (0) | 2025.05.28 |
| 적립식 수익률을 거치식 수익률로 환산해서 비교하기 (울프럼 알파 vs 챗GPT + 제미나이 + 코파일럿) (0) | 2025.05.27 |
| [중급 24] 베이즈 정리와 추론 - 나주사씨의 친구들은 주사위를 어떻게 추정했을까? (고정된 수익률 분포를 완벽하게 아는 경우) (0) | 2025.05.26 |
| [중급 23] 숨겨진 주사위는 몇 면일까? (모집단의 추정) (0) | 2025.05.25 |
| [중급 22] 투자 정보의 가치는 얼마일까? (누군가 내일의 주가 수익률을 알려준다면 초모험씨는 얼마까지 지불할 수 있을까?) (0) | 2025.05.25 |




