지금까지 파이썬을 이용하여 두 가지 종류의 그래프를 그리는 방법을 살펴보았습니다. 시간의 흐름에 따른 변화를 파악하기에 편리한 선 그래프와 확률 분포를 나타내는데 유용한 히스토그램(histogram; 도수분포그래프)이었습니다. 히스토그램은 일종의 막대그래프입니다. 파이썬은 막대그래프를 위한 함수도 별도로 제공합니다. 이 외에도 원(파이) 그래프나 등고선 그래프도 그릴 수 있습니다. 참고: Plot types - Matplotlib
투자 성과 분석에서 특히 유용한 그래프 중 하나는 산점도(scatter plot; 분산형 차트)입니다. 2차원 산점도라면 자산의 특성을 나타내는 두 가지 값을 각각 x값과 y값으로 하는 2차원 평면 그래프입니다.
산점도는 자산의 특성값에 해당되는 위치에 자산을 나타낼 수 있고, 자산 간의 상대 비교에 편리한 그래프입니다. 특히 평균-분산 그래프와 같이 자산에 분산 투자했을 때의 효과를 시각적으로 표시하기에도 유용합니다.
이 글에서는 주식과 예금을 산점도 그래프에 그려보고, 주식과 예금의 분산 투자 효과를 어떻게 나타낼 수 있는지 살펴봅니다.

주의: 이 글은 특정 상품 또는 특정 전략에 대한 추천의 의도가 없습니다. 이 글에서 제시하는 수치는 과거에 그랬다는 기록이지, 앞으로도 그럴 거라는 예상이 아닙니다. 분석 대상, 기간, 방법에 따라 전혀 다른 결과가 나올 수 있습니다. 데이터 수집, 가공, 해석 단계에서 의도하지 않은 오류가 있을 수 있습니다. 일부 설명은 편의상 현재형으로 기술하지만, 데이터 분석에 대한 설명은 모두 과거형으로 이해해야 합니다.
산점도에서 자산의 표현
다음은 SPY의 수정 종가를 가져와서 1년(252거래일) 수익률의 평균과 표준 편차를 계산하는 코드입니다.
spy = fdr.DataReader('SPY')['Adj Close']
spy_252 = spy.pct_change(252)
spy_252_mean = spy_252.mean()
spy_252_std = spy_252.std()오랜만에 접속해서 이 코드를 입력하고 실행하면 에러가 발생할 수 있습니다. 다음과 같이 fdr이 무엇인지 모르겠다는 메시지가 나타날 수 있습니다.
NameError: name 'fdr' is not defined코랩에 다시 접속할 때, 이전 서버가 아닌 새로운 서버로 할당되었기 때문입니다. 공통으로 사용할 다음과 같은 코드는 노트북의 첫 셀에 넣어 두고 필요한 경우 재실행하면 편리합니다.
!pip install -q finance-datareader
import FinanceDataReader as fdr
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
import pandas as pd
from matplotlib.ticker import PercentFormatter
from scipy.stats import norm
mpl.rcParams.update({"axes.grid" : True})산점도를 그리는 함수는 plt.scatter()입니다. 다음과 같이 사용하면 됩니다.
plt.scatter(spy_252_std, spy_252_mean)
plt.xlim(0, 0.18)
plt.ylim(0, 0.14)
plt.gca().xaxis.set_major_formatter(PercentFormatter(xmax = 1, decimals = 0))
plt.gca().yaxis.set_major_formatter(PercentFormatter(xmax = 1, decimals = 0))x값으로 SPY 1년 수익률의 표준 편차를, y값으로 1년 수익률의 평균을 나타냈기에, 평균-분산 그래프가 됩니다. 그래프의 x축과 y축 범위를 지정하고, 수치에는 퍼센트(%) 기호를 붙였습니다. 다음과 같은 결과를 얻을 수 있습니다.

이제 은행 예금을 추가해 보겠습니다. 예금은 변동성이 없는 자산이기에 표준 편차가 0%입니다. 예금 이율을 2%로 가정하고 추가해 봅니다.
plt.scatter(spy_252_std, spy_252_mean, label = 'SPY')
plt.scatter(0, 0.02, label = 'Bank')
plt.xlim(0, 0.18)
plt.ylim(0, 0.14)
plt.gca().xaxis.set_major_formatter(PercentFormatter(xmax = 1, decimals = 0))
plt.gca().yaxis.set_major_formatter(PercentFormatter(xmax = 1, decimals = 0))
plt.legend(loc = 'upper left')
plt.show()은행 예금에 해당되는 (0, 2%)에 점을 추가로 찍었습니다. SPY와 Bank를 범례에 보여줄 이름(label)도 추가했습니다. plt.legend()는 대개는 그래프 내용을 가리지 않는 적절한 위치에 범례를 표시하지만, 간혹 애매한 위치에 나타나거나 더 나은 위치가 있을 수 있습니다. 여기서는 loc 인자로 상단 왼쪽에 범례를 표시하도록 지정했습니다.

하단 왼쪽에 오렌지색으로 표시된 예금이 보입니다.
산점도에서 분산 투자 효과의 표현
이제 분산 투자 효과를 살펴보겠습니다. SPY에 투자금 일부를 투자하고 나머지는 예금에 두어 2% 이자를 받는 것입니다. SPY 투자 비중을 w = 70%로 두면, 포트폴리오는 SPY 1년 수익률의 70%를 얻고, 예금 수익률(2%)에서 30%를 받게 됩니다. 수식으로는 SPY × w + Bank × (1 - w)가 됩니다.
코드로는 다음과 같이 됩니다. 그래프의 축 범위 등을 지정하는 코드는 동일하기에 생략했습니다.
plt.scatter(spy_252_std, spy_252_mean, label = 'SPY')
plt.scatter(0, 0.02, label = 'Bank')
port = spy_252 * 0.7 + 0.02 * 0.3
plt.scatter(port.std(), port.mean(), label = 'Portfolio')
# 이하 생략포트폴리오 수익률은 spy_252 * 0.7 + 0.02 * 0.3으로 계산하면 됩니다. SPY 수익률 70%와 예금 수익률 30%를 합한 것입니다.
spy_252는 하나의 수치가 아니라 1년(252거래일) 수익률의 배열(여기서는 Series)입니다. SPY 수익률 각각의 값에 70%를 곱하고, 예금 수익률 2%의 30%인 0.6%를 더한 새로운 배열을 만들어서 port라고 이름을 붙였습니다. 이 배열의 표준 편차와 평균으로 점을 찍으면 다음과 같이 됩니다.

그래프에 나타난 초록색 점이 SPY에 70%, 예금에 30% 비중으로 투자한 포트폴리오의 위치입니다. 예금은 변동성이 없는 자산이기에, SPY과 예금 혼합 시 평균 수익률과 표준 편차 모두 7 : 3인 위치에 포트폴리오가 나타나게 됩니다.
이제 2% 단위로 세세하게 조정한 포트폴리오를 그려봅니다.
plt.scatter(spy_252_std, spy_252_mean, label = 'SPY')
plt.scatter(0, 0.02, label = 'Bank')
for w in np.arange(0.02, 1, 0.02):
port = spy_252 * w + 0.02 * (1 - w)
plt.scatter(port.std(), port.mean(), s = 5)
# 이하 생략SPY 투자 비중 w를 변경해 가며 그려야 하기에 for 문장을 사용했습니다. np.arange(0.02, 1, 0.02)는 0.02부터 1이 되기 직전까지 0.02 단위로 값을 생성하라는 의미입니다. 2%, 4%, ..., 98%까지 생성됩니다. for 문장의 기본 정의가 끝나고 다음부터 반복 실행해야 하는 내용을 표시한다는 의미로 콜론(:)이 마지막에 있습니다.
그 아래에는 반복할 명령들이 나열되어 있습니다. for 문장의 하위 구문이기에 2개의 빈칸으로 들여쓰기로 표시되어 있습니다. 파이썬은 들여쓰기로 명령문의 구조를 지시합니다.
반복되는 부분을 보면, 먼저 w값에 대해 포트폴리오의 수익률 배열을 구합니다. 수익률 배열의 표준 편차와 평균을 구해 점을 찍습니다. SPY와 예금보다 작은 크기의 점을 그리기 위해 크기(size)를 5로 지정했습니다. 기본 크기는 40입니다.
그 이하는 앞서와 동일합니다. 실행하면 다음과 같은 그래프가 나옵니다.
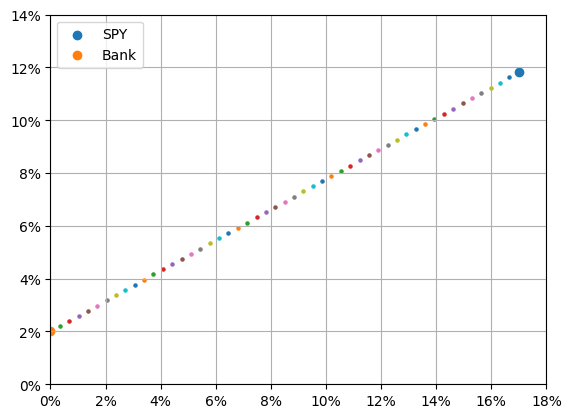
plt.scatter()는 한 번 불릴 때마다 색이 바뀝니다. 색을 쓰는 순서를 팔레트(palette)라고 하는데 모든 색을 다 쓰고 나면 처음부터 다시 씁니다. 기본 팔레트는 10개의 색상이 정의되어 있고, 필요하다면 다른 팔레트를 바꿀 수도 있습니다. 색을 직접 지정하고 싶은 경우에는 c = 'COLOR'로 지정하면 됩니다.
평균-분산 그래프를 그리는 방법은 이게 전부라고 해도 과언이 아닙니다. 여기서 하나의 자산은 변동성이 없는 예금이기에 간단해 보이는 것입니다. 자산의 수를 늘리면 됩니다.
분산 투자한 포트폴리오의 특성이 왜 이렇게 나타나고, 어떻게 해석할 수 있는지는 이보다 훨씬 긴 설명이 필요합니다. 명확하게 이해하고 분석해서 결과를 해석하기를 권합니다. 이에 대해서는 책 <왜 위험한 주식에 투자하라는 걸까 - 장기 투자와 분산 투자에 대한 통계학적 시각>을 참고하기 바랍니다.
정리하며
파이썬으로 산점도를 그리는 예를 살펴보았습니다. 산점도는 평균-분산 그래프와 같은 형식으로 개별 자산 및 여러 자산에 분산 투자한 포트폴리오의 특성을 쉽게 표현하고 비교할 수 있어 투자 성과 분석에 유용합니다.
이 글에서는 변동성이 없는 예금과의 혼합을 다루었습니다. 이어지는 글에서는 변동성이 있는 두 자산의 혼합 결과를 평균-분산 그래프로 나타내보고, 분산 투자로 수익률 분포가 어떻게 변했는지 살펴봅니다.
참고: 연재와 관련한 질문은 댓글로 남겨주시기 바랍니다. 답변을 드리거나 이후 연재에서 다룰 수 있도록 노력하겠습니다.
참고 서적: 왜 위험한 주식에 투자하라는 걸까? - 장기 투자와 분산 투자에 대한 통계학적 시각
이어지는 글: [파이썬 분석 7] 두 가지 자산을 혼합해보고, 수익률 분포의 변화를 살펴보자
연재 목록: 자산 배분 분석 방법 책 소개, 연재글 및 사례 모음 [목록]
함께 읽으면 좋은 글 (최신 글)
- [파이썬 분석 5] 환율을 적용해 보고 어떤 변화가 발생했는지 살펴보자
- [파이썬 분석 4] 수익률의 기초 통계량을 추출해 보고 확률 분포를 그려보자
- [파이썬 분석 3] 누적 수익률로 그래프로 그려 보자 (로그 스케일에 수익률을 표현하는 방법)
- [파이썬 분석 2] PR(배당 미고려)과 TR(배당 재투자) 주가 흐름을 그래프로 그려 보자 (FinanceDataReader 모듈 사용)
- [파이썬 분석 1] 주가 흐름을 그래프로 그려 보자 (구글 코랩을 써 보자! 인공지능 너도 실수하는구나?)
함께 읽으면 좋은 글 (인기 글)
'주식투자' 카테고리의 다른 글
| [파이썬 분석 10] 사용자 포트폴리오를 나타내 보고, 특정 위치의 포트폴리오의 투자 비중을 살펴보자 (0) | 2025.04.16 |
|---|---|
| [파이썬 분석 9] 세 가지 자산에 분산 투자한 결과를 분석해 보자 (+결과 재사용을 위한 함수 정의) (0) | 2025.04.15 |
| [파이썬 분석 8] 세 가지 자산에 분산 투자한 결과를 살펴보자 (+재사용을 위한 함수 정의) (2) | 2025.04.14 |
| [파이썬 분석 7] 두 가지 자산을 혼합해 보고, 수익률 분포의 변화를 살펴보자 (0) | 2025.04.14 |
| [파이썬 분석 5] 환율을 적용해 보고 어떤 변화가 발생했는지 살펴보자 (0) | 2025.04.13 |
| [파이썬 분석 4] 수익률의 기초 통계량을 추출해 보고 확률 분포를 그려보자 (0) | 2025.04.12 |
| [파이썬 분석 3] 누적 수익률로 그래프로 그려 보자 (로그 스케일에 수익률을 표현하는 방법) (0) | 2025.04.12 |
| [파이썬 분석 2] PR(배당 미고려)과 TR(배당 재투자) 주가 흐름을 그래프로 그려 보자 (FinanceDataReader 모듈 사용) (0) | 2025.04.12 |




