이전 글에서 평균-분산 그래프에 표시할 포트폴리오의 성과를 계산하는 함수를 독립시켰습니다. 이 함수의 역할이 퀀트 투자에서 흔히 말하는 백테스트(backtest) 즉 일종의 시뮬레이션(모의실험)입니다. 모든 백테스트 함수의 구조는 거의 동일합니다. 이 연재에서는 신뢰성이 높다고 볼 수 있는 주가 데이터만으로 백테스트를 하기에 간단해 보이지만, 현실에서는 백테스트를 위한 데이터 구축부터 큰 난항을 겪게 될 가능성이 다분합니다. 이전 글: [파이썬 분석 9] 세 가지 자산에 분산 투자한 결과를 분석해 보자 (+결과 재사용을 위한 함수 정의)
이제 투자자의 궁금증을 해소해 볼 차례입니다. 내가 고려하고 있는 또는 지금 사용하고 있는 자산 비중의 포트폴리오는 어디쯤 위치하는 것일까요? 평균-분산 그래프에서 특정 위치가 괜찮아 보이는데, 그 영역의 일반적인 투자 비중은 무엇일까요?

주의: 이 글은 특정 상품 또는 특정 전략에 대한 추천의 의도가 없습니다. 이 글에서 제시하는 수치는 과거에 그랬다는 기록이지, 앞으로도 그럴 거라는 예상이 아닙니다. 분석 대상, 기간, 방법에 따라 전혀 다른 결과가 나올 수 있습니다. 데이터 수집, 가공, 해석 단계에서 의도하지 않은 오류가 있을 수 있습니다. 일부 설명은 편의상 현재형으로 기술하지만, 데이터 분석에 대한 설명은 모두 과거형으로 이해해야 합니다.
그래프를 그리는 공통 코드로 함수 정의
매번 그래프를 그리고 설정하는 데 사용하는 공통 코드로 fill_graph_basics()라는 함수를 정의합니다.
def fill_graph_basics(_df, _port_df):
for col in _df.columns:
plt.scatter(_df[col].std(), _df[col].mean(), label = col)
plt.scatter(_port_df.Std, _port_df.Mean, s = 5, c = 'tab:cyan', alpha = 0.2, label = 'ALL')
plt.gca().xaxis.set_major_formatter(PercentFormatter(xmax = 1, decimals = 0))
plt.gca().yaxis.set_major_formatter(PercentFormatter(xmax = 1, decimals = 0))
plt.xlim(0.08)
plt.ylim(0.04)
plt.legend()이전 글에서 작성한 코드 중에서 반복해서 사용할 코드만 모았습니다. 인자로 자산의 수익률(252일)과 생성한 포트폴리오 평가 결과를 담은 DataFrame을 받았습니다. 각 자산의 위치를 평균-분산 그래프에 나타내고, 전체 포트폴리오는 배경처럼 반투명한 시안색으로 깔았습니다. x축과 y축을 퍼센트 단위로 설정했습니다.
xlim()과 ylim()으로 x축과 y축의 최소값을 지정했는데, 이는 연재에 사용할 그림에서 포트폴리오 영역을 크게 표시하기 위해 의도적으로 설정한 것입니다. 일반적인 분석에서는 이를 인지하고 분석하거나 각각 0으로 두어야 시각적 착시를 줄일 수 있습니다. 마지막으로 범례를 붙였습니다.
다음과 같이 코드를 실행하면 기본 그래프를 그려줍니다. 함수 내에서 항상 x, y축 이름도 달도록 지정할 수 있습니다.
fill_graph_basics(df252, port_df)
사용자 포트폴리오 계산을 위한 함수 확장
이제 사용자 포트폴리오의 위치를 나타내 보겠습니다. 예를 들어 SPY에 60%, TLT와 GLD에는 각각 20%씩 투자한 포트폴리오는 어디쯤인지 알고 싶을 수 있습니다.
이전에 정의한 calc_ports() 함수는 주어진 횟수만큼 임의의 투자 비중을 만들어서 계산한 포트폴리오 결과를 돌려줍니다. 투자 비중을 지정하면 해당 투자 비중으로 한 번만 수행하도록 바꾸어 보겠습니다.
def calc_ports(_df, _count = 1000, _my_w = None):
_w_l = []
_mean_l = []
_std_l = []
for _ in range(_count):
_w = np.random.random(len(_df.columns))
if _my_w is not None:
_w = np.array(_my_w).astype(float)
_w /= _w.sum()
_port = (_df * _w).sum(axis = 1)
_w_l.append(_w)
_mean_l.append(_port.mean())
_std_l.append(_port.std())
if _my_w is not None:
break
_w_df = pd.DataFrame(_w_l, columns = _df.columns)
_stat_df = pd.DataFrame({'Mean': _mean_l, 'Std': _std_l})
_port_df = pd.concat([_w_df, _stat_df], axis = 1)
return _port_df대부분의 코드가 동일합니다. 변경된 부분 위주로 살펴봅니다.
def calc_ports(_df, _count = 1000, _my_w = None):사용자 투자 비중을 _my_w에 지정할 수 있도록 함수를 정의하였습니다. 사용자 투자 비중이 지정되지 않으면 값이 없다는 None이 들어갑니다.
_w = np.random.random(len(_df.columns))
if _my_w is not None:
_w = np.array(_my_w).astype(float)기본으로 임의 생성한 투자 비중을 사용합니다. 만일 사용자 지정 투자 비중이 있다면(if _my_w is not None:), 이를 대신 사용합니다. 사용자가 지정한 투자 비중을 실수(float) 배열로 만들어서 _w를 재설정합니다.
if _my_w is not None:
break사용자 지정 투자 비중이 있다면, 여러 번 계산할 필요가 없습니다. 동일한 투자 비중이니 결과가 항상 같을 것이기 때문입니다. for 루프(loop)를 반복하지 않고 빠져나오기 위해 break 구문을 사용했습니다.
참고: 이 코드는 구조적으로 깔끔하게 정리된 것이 아닙니다. 주어진 투자 비중에 대해 포트폴리오를 계산하는 함수(func1)를 독립시키고, 임의로 투자 비중을 여럿 만들어서 func1을 호출하는 func2를 정의하는 것이 구조적으로 조금 더 적절합니다. 이 연재는 파이썬 언어를 소개하는 글이 아니기에, 기존 코드를 최대한 재사용하는 방식으로 수정하였습니다.
사용자 지정 투자 비중으로 함수를 호출할 수도 있고, 이전과 동일하게 임의 포트폴리오를 만들 수도 있습니다.
calc_ports(df252, _my_w = [60, 20, 20])calc_ports(df252, _count = 100)
사용자 포트폴리오의 표시
이제 사용자 지정 포트폴리오를 나타내 보겠습니다. 두 개의 포트폴리오를 생각해 보겠습니다. 포트폴리오1은 전통적인 6 : 4 포트폴리오로 SPY에 60%, TLT에 40%로 투자합니다. 포트폴리오2는 SPY, TLT, GLD에 60%, 20%, 20% 비중으로 투자하는 경우라고 해 보겠습니다.
fill_graph_basics(df252, port_df)
port1 = calc_ports(df252, _my_w = [60, 40, 0])
plt.scatter(port1.Std, port1.Mean, s = 100, marker = '*', label = 'Port1')
port2 = calc_ports(df252, _my_w = [60, 20, 20])
plt.scatter(port2.Std, port2.Mean, s = 100, marker = 'X', label = 'Port2')
plt.legend()전체 가능했던 포트폴리오 중에서 두 포트폴리오의 위치는 다음과 같이 표시됩니다.

plt.scatter() 함수를 호출할 때, marker를 지정했습니다. 포트폴리오1은 별(*) 표시로, 포트폴리오2는 가위(X) 표시로 나타냈습니다.
포트폴리오1은 좀 아쉽습니다. 위쪽으로 보면 동일한 변동성으로 더 연 1% 정도 더 높은 수익률을 얻을 수 있었던 포트폴리오가 존재했습니다. 왼쪽으로 보아도 동일한 수익률도 1% 정도 변동성이 낮았던 포트폴리오가 있었습니다. 참고: 포트폴리오가 하나인 것처럼 설명하지만, 포트폴리오들의 평균을 말합니다.
이에 비해 포토폴리오2는 괜찮은 편이었다고 할 수 있습니다. 전체 포트폴리오 집합의 왼쪽 상단 외곽선인 효율적 투자선(efficient frontier) 근처에 위치하고 있기 때문입니다.
관심 있는 영역에 위치한 포트폴리오의 특성
투자자는 표준 편차와 수익률 모두 10% 정도였던 포트폴리오에 관심이 있다고 하겠습니다. 이 부분을 다른 색으로 표시해 보겠습니다. 다음 코드를 추가하면 됩니다.
extend = 0.5 / 100
cond = (port_df.Std <= (0.1 + extend)) & (port_df.Mean >= (0.1 - extend))
sel_port_df = port_df[cond]
plt.scatter(sel_port_df.Std, sel_port_df.Mean,
s = 0.1, c = 'tab:green', alpha = 0.8, label = 'Interesting Ports')관심 있는 포트폴리오의 위치는 표준 편차 10%, 수익률 10%인 지점입니다. 이 점을 중심으로 ±0.5%(extend) 이내에 있는 포트폴리오를 찾아 초록색으로 표시합니다. 다음과 같은 결과가 나옵니다.

관심 영역에 포함된 포트폴리오는 sel_port_df에 있습니다. 다음과 같이 출력해 볼 수 있습니다.
sel_port_df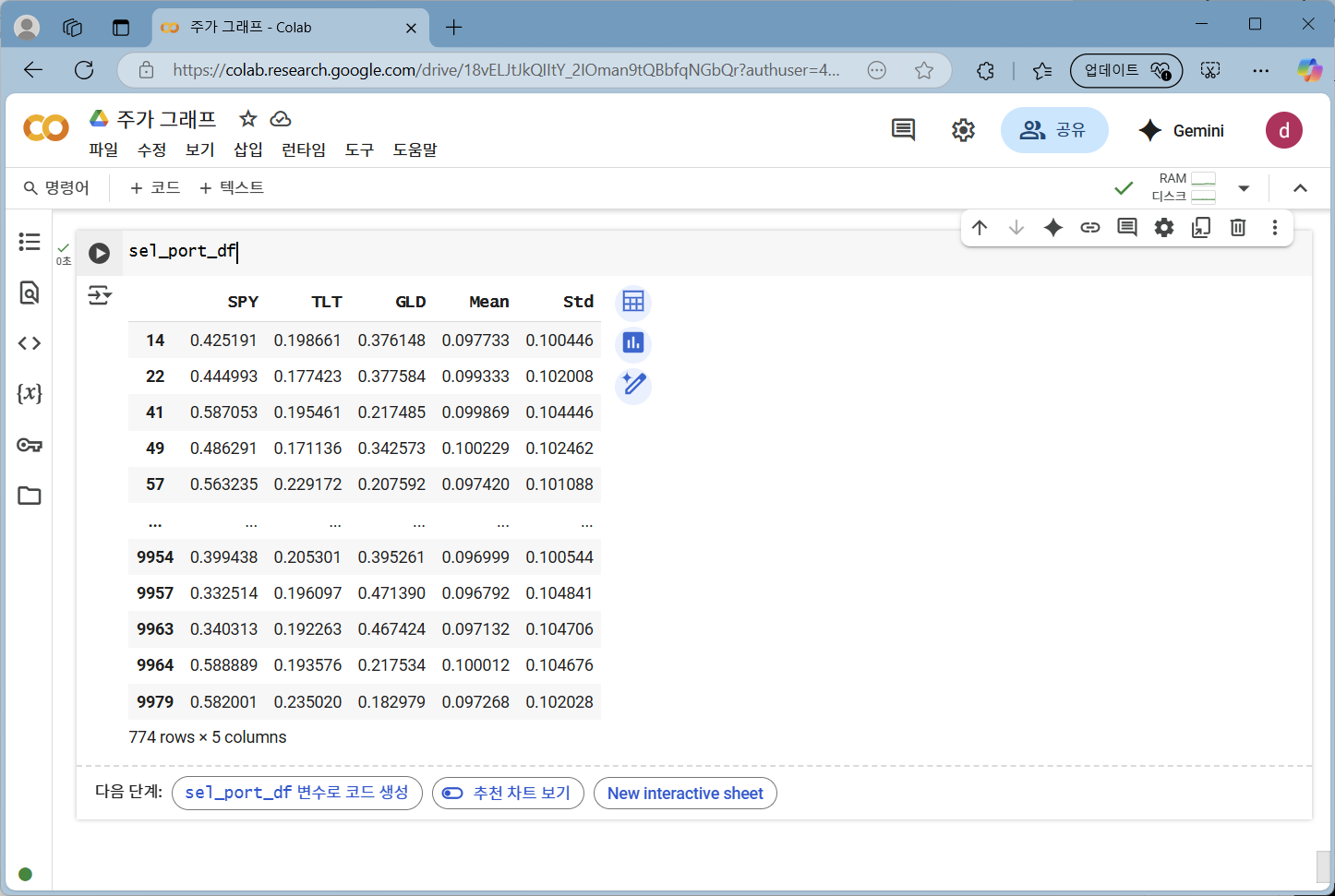
774개나 되는 포트폴리오가 있습니다. 총 10,000개의 랜덤 포트폴리오를 생성했으니 7.74%나 됩니다.
SPY 비중이 30%인 경우도 있고, 60%에 근접하는 경우도 있습니다. TLT는 대략 20% 내외인 듯합니다. GLD 역시 20% 정도부터 50%에 가까운 경우까지 다양합니다. 확률 분포로 그려보면 각 자산 비중의 대략적인 분포를 보다 쉽게 파악할 수 있습니다.
plt.hist(sel_port_df[['SPY', 'TLT', 'GLD']],
bins = 50, density = True, histtype = 'step',
label = sel_port_df.columns)
plt.gca().xaxis.set_major_formatter(PercentFormatter(xmax = 1, decimals = 0))
plt.legend(reverse = True)
plt.show()plt.hist() 함수로 확률 분포를 그렸습니다. 코드가 여러 줄로 되어 있지만, 한 줄에 써도 됩니다. 휴대폰으로 이 글을 읽으시는 분들이 위해 줄을 나눈 것입니다.

파란색 SPY는 30%에서 65% 정도까지 분포되어 있습니다. 오렌지색 TLT는 15% 정도에서 30%에 조금 안 되는 정도까지 있습니다. 초록색 GLD는 10%에서 50% 가까이 범위가 넓습니다.
관심 영역의 크기는 포트폴리오 전체 영역과 비교하면 상당히 작습니다. 그러니 투자자는 해당 영역에 꽤 비슷한 투자 비중을 가진 포트폴리오가 모여있을 거라 상상했을 수 있습니다.
현실은 달랐습니다. 투자 비중만 따져본다면, 도무지 비슷하다고 보기 어려운 다양한 포트폴리오가 밀집되어 있는 것입니다. 만일 미래에도 SPY, TLT, GLD의 경향이 어느 정도 비슷하게 나타날 거라 생각한다면, 투자자는 어떤 포트폴리오를 선택하는 것이 합리적일까요?
정리하며
평균-분산 그래프에 사용자 지정 포트폴리오의 위치를 나타내 보았습니다. 평균-분산 그래프는 개별 포트폴리오의 상대적 위치를 표현하기에, 사용자 지정 포트폴리오보다 더 나았던 포트폴리오가 있었는지, 있었다면 어느 정도 차이가 났는지를 한눈에 살펴보기 용이합니다.
투자자가 관심을 가지는 성과를 보였던 포트폴리오 영역이 있다면, 해당 영역을 그래프에 표시할 수도 있고, 영역 내 포트폴리오들의 구체적인 투자 비중을 살펴볼 수도 있습니다. 하지만 투자자의 기대와는 달리 투자 비중은 균질적이지 않을 수 있습니다.
과거 데이터를 참고하여 투자 비중을 결정하고자 하는 투자자에게는 난감한 상황이 발생할 수 있는 것입니다. 자산의 수가 2개인 경우에는 포트폴리오 궤적은 선의 형태를 만들기에, 투자자가 수익과 위험을 적절히 고려하여 결정하기 어렵지 않을 수 있습니다.
하지만 보다 많은 수의 자산을 고려하면, 자산의 성격과 자산 간 관계에 따라서는 비슷한 투자 비중이라 볼 수 없는 포트폴리오들이 같은 지역에 뭉쳐있을 수 있습니다. 투자자는 어떻게 해야 할까요? 이 문제는 파이썬으로 그래프를 그리는 방법을 소개하는 이 연재의 범위를 벗어나기에 추가로 다루지는 않습니다. 따로 진행하는 투자 성과 분석 중급편 연재에서 살펴볼 계획입니다.
참고: 연재와 관련한 질문은 댓글로 남겨주시기 바랍니다. 답변을 드리거나 이후 연재에서 다룰 수 있도록 노력하겠습니다.
참고 서적: 왜 위험한 주식에 투자하라는 걸까? - 장기 투자와 분산 투자에 대한 통계학적 시각
이어지는 글: [파이썬 분석 11] 장기 투자에 보다 적합한 복리 수익률을 구해보자 (통계량의 주관성)
연재 목록: 자산 배분 분석 방법 책 소개, 연재글 및 사례 모음 [목록]
함께 읽으면 좋은 글 (최신 글)
함께 읽으면 좋은 글 (인기 글)
'주식투자' 카테고리의 다른 글
| [파이썬 분석 14] 두 자산의 성과를 비교해 보자 (TIGER 미국배당다우존스와 TIGER 미국배당다우존스타겟커버드콜2호) (0) | 2025.04.19 |
|---|---|
| [파이썬 분석 13] 시간이 흐름에 따른 주가의 변화는 표현해 보자 (이동 평균, 하위 순위 주가, +rolling()) (0) | 2025.04.18 |
| [파이썬 분석 12] 위험 척도를 하나 더 표현해 보자 (+컬러맵 사용) (0) | 2025.04.17 |
| [파이썬 분석 11] 장기 투자에 보다 적합한 복리 수익률을 구해보자 (통계량의 주관성) (0) | 2025.04.17 |
| [파이썬 분석 9] 세 가지 자산에 분산 투자한 결과를 분석해 보자 (+결과 재사용을 위한 함수 정의) (0) | 2025.04.15 |
| [파이썬 분석 8] 세 가지 자산에 분산 투자한 결과를 살펴보자 (+재사용을 위한 함수 정의) (2) | 2025.04.14 |
| [파이썬 분석 7] 두 가지 자산을 혼합해 보고, 수익률 분포의 변화를 살펴보자 (0) | 2025.04.14 |
| [파이썬 분석 6] 산점도(scatter plot)에 자산의 특성을 나타내고, 예금과 혼합 효과도 표현해 보자 (0) | 2025.04.13 |




