지난 두 편의 글을 통해 두 자산에 분산 투자한 포트폴리오의 복리 수익률(compound return) 특성을 살펴보았습니다. 선형 수익률(linear return)의 산술 평균을 이용한 평균-분산 그래프에서는 포트폴리오 수익률이 선형적으로 변하지만, 복리 수익률은 변동성이 감소할 때 크던 작든 증가하는 현상이 발생합니다. 장기 수익률을 높이고자 복리 투자자는 복리 수익률로 그린 평균-분산 그래프를 참고해야 하는 주된 이유입니다.
- [중급 40] 수익률이 로그 정규 분포를 따르는 두 자산에 분산 투자하면 어떻게 될까? (완전 선형 관계인 경우)
- [중급 41] 수익률이 로그 정규 분포를 따르는 두 자산에 분산 투자하면 어떻게 될까? (완전 독립 관계인 경우)
이 글에서는 SPY, TLT, GLD 세 자산에 분산 투자했을 때의 효과를 복리 수익률로 그린 평균-분산 그래프로 살펴봅니다.

주의: 이 글은 특정 상품 또는 특정 전략에 대한 추천의 의도가 없습니다. 이 글에서 제시하는 수치는 과거에 그랬다는 기록이지, 앞으로도 그럴 거라는 예상이 아닙니다. 분석 대상, 기간, 방법에 따라 전혀 다른 결과가 나올 수 있습니다. 데이터 수집, 가공, 해석 단계에서 의도하지 않은 오류가 있을 수 있습니다. 일부 설명은 편의상 현재형으로 기술하지만, 데이터 분석에 대한 설명은 모두 과거형으로 이해해야 합니다.
선형 수익률의 산술 평균으로 그린 평균-분산 그래프
다음은 SPY + TLT + GLD 포트폴리오의 선형 수익률로 산술 평균을 계산하여 그린 평균-분산 그래프입니다.
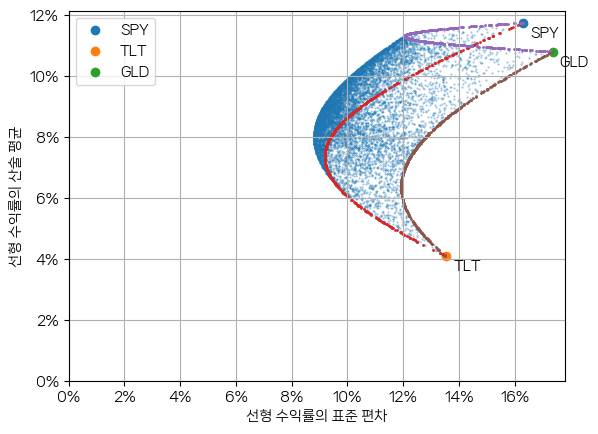
그림에서 작은 파란색 점으로 이루어진 영역이 SPY + TLT + GLD 분산 투자 포트폴리오들입니다. 두 자산에 분산 투자한 포트폴리오 궤적은 세 곡선으로 표시되어 있습니다.
포트폴리오의 선형 수익률은 세 자산 각각의 평균 수익률의 투자 비중에 따른 가중 평균이기에 모든 포트폴리오는 평균 수익률이 가장 높았던 SPY와 가장 낮았던 TLT 사이에 위치하게 됩니다. 이에 비해 표준 편차는 자산 간의 관계에 따라 개별 자산의 표준 편차보다 줄어들 수 있습니다.
이 그래프를 해석한 투자자가 가장 높은 수익률을 기대한다면, SPY에 100% 비중으로 투자하게 될 것입니다. 만일 최소 분산 포트폴리오나 최대 샤프 비율(Sharpe Ratio) 포트폴리오를 선택한다면 다른 위치의 포트폴리오를 고르게 될 것입니다. 참고: 최대 샤프 비율 포트폴리오는 MVO(Mean-Variance Optimization; 평균-분산 최적화) 포트폴리오라고 부릅니다.
다음은 최대 평균, 최소 분산 포트폴리오와 예금 이율은 2%로 가정했을 때의 최대 샤프 비율 포트폴리오를 평균-분산 그래프에 표시한 결과입니다.
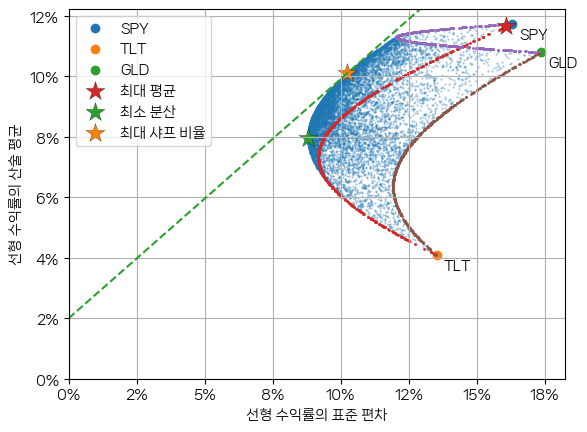
빨간색 별 형태의 최대 평균 포트폴리오는 SPY에 100% 비중으로 투자하는 포트폴리오입니다. 참고: 투자 비중을 임의로 생성한 1만개의 포트폴리오로 시뮬레이션한 결과에서 골랐습니다. 정확하게 SPY에 100% 비중으로 투자한 포트폴리오가 생성되지 않았기에, SPY 위치에서 살짝 벗어나 있습니다.
초록색 별 모양의 최소 분산 포트폴리오는 약 9%의 표준 편차를 가졌습니다. 샤프 비율이 최대인 오렌지색 포트폴리오는 (0, 2%) 위치에 있는 예금과 파란색 포트폴리오 영역과의 접선(tangent line) 위에 있는 포트폴리오입니다.
복리 수익률로 그린 평균-분산 그래프
동일한 결과를 로그 수익률(log return)을 사용하여 평균-분산 그래프를 그려봅니다. 로그 수익률의 평균과 복리 수익률은 강한 증가함수(strictly increasing function) 관계이며, 상호 변환이 가능합니다. 로그 수익률의 평균은 (1 + 복리 수익률)의 로그 값이기 때문입니다.
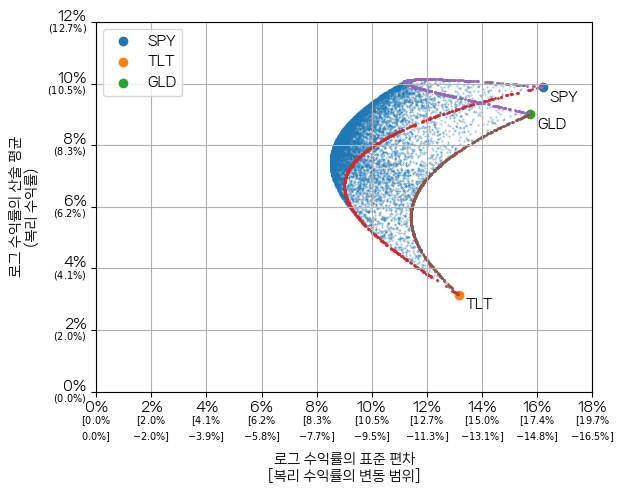
x와 y축의 기본 눈금은 로그 수익률입니다. 괄호 안에 든 작은 수치는 해당 로그 수익률에 대응하는 복리 수익률입니다. 로그 수익률과 복리 수익률의 관계는 [중급 39] 복리 수익률로 보는 평균-분산 그래프의 해석 (표준 편차에 대한 비대칭 해석)를 참고하기 바랍니다.
전반적으로 변동성이 줄어들수록 로그 수익률(복리 수익률)이 증가하는 방향으로 부풀어 오르는 것을 알 수 있습니다.
최대 평균, 최소 분산, 최대 샤프 비율 포트폴리오의 위치를 표시하면 다음과 같습니다.
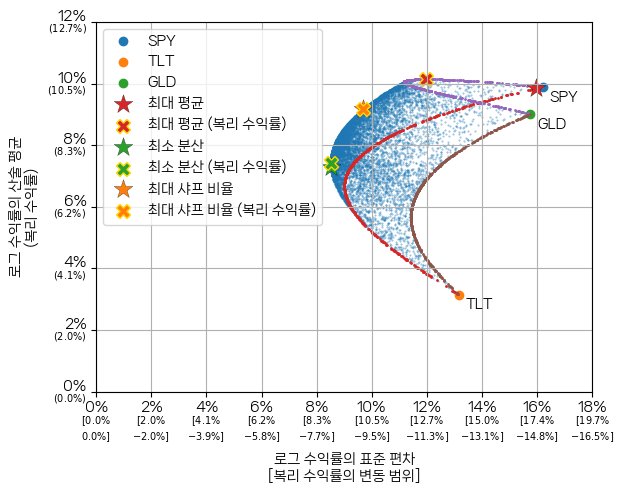
별 모양으로 표시된 포트폴리오는 앞에서 선형 수익률의 산술 평균으로 구한 세 가지 포트폴리오입니다. 가위표 모양으로 표시된 포트폴리오는 로그 수익률로 계산한 세 포트폴리오입니다.
최소 분산 포트폴리오는 위치 변동이 거의 없습니다. 이 사례에 한하기는 하지만, 선형 수익률로 계산한 변동성과 로그 수익률로 계산한 변동성의 상대적인 경향이 크게 다르지 않았기 때문입니다. 마찬가지로 최소 분산 포트폴리오의 위치도 별다른 변화가 없습니다.
평균 수익률을 최대화하는 포트폴리오는 의미 있는 위치 변동이 있었습니다. 선형 수익률로 볼 때에는 SPY 100% 투자하는 포트폴리오가 선택되었지만, 복리 수익률로 볼 때에는 대략 SPY에 68%, GLD에 32% 투자하는 포트폴리오가 더 높은 수익률을 보였습니다.
SPY 68% + GLD 32%는 복리 수익률만 높아지지 않았습니다. 이 포트폴리오는 SPY 대비 대략 1 - 12% / 16% = 1 - 3 / 4 = 25%가량 변동성이 낮았습니다. 장기 복리 투자자라면, 복리 수익률은 더 높으면서 변동성까지 낮은 이 포트폴리오를 선택하는 것이 합리적입니다.
정리하며
선형 수익률의 산술 평균으로 그린 평균-분산 그래프와 복리 수익률로 그린 평균-분산 그래프를 비교해 보았습니다. SPY, TLT, GLD에 분산 투자하는 포트폴리오에 한정한다면, 최소 분산, 최대 샤프 비율 포트폴리오의 위치는 비슷했지만, 최대 평균 포트폴리오는 의미 있는 차이가 있었습니다.
복리 수익률로 그린 평균-분산 그래프는 복리 수익률을 보다 면밀하게 추정할 수 있고, 변동성에 의한 수익률 영향도 함께 살펴볼 수 있습니다. 장기 복리 투자자가 포트폴리오를 선택하는데 참고하기에 보다 적절한 그래프입니다.
참고 도서:
이어지는 글: [중급 43] 동일하다는 것은 어떻게 판별할 수 있을까? (다른 동전을 던져 만든 주가 그래프는 같은 것일까? 하나씨와 두나씨의 투자)
목차: [연재글 목차] 투자 성과 분석 (기초편, 초급편, 중급편): 순서대로 차근차근 읽으면 좀 더 이해가 쉽습니다.
함께 읽으면 좋은 글 (최신 글)
- NVDY 배당금과 동일한 현금 흐름을 NVDA(기초자산) 매도로 만들때의 실수익률을 구해 보자 (XIRR() 함수를 이용한 내부 수익률) [데이터 분석 부록 C6]
- TSLY의 배당금과 세금을 고려한 실수익률을 구해 보자 (XIRR() 함수를 이용한 내부 수익률) [데이터 분석 부록 C5]
- 구글 시트로 배당을 고려한 내부 수익률을 구해 보자 (TIGER 미국배당다우존스타겟커버드콜2호 + XIRR() 함수 사용) [데이터 분석 부록 C4]
- 구글 시트와 마이크로소프트 엑셀에서 XIRR() 함수로 투자 기록에서 거치식 CAGR 구하기 [데이터 분석 부록 C3]
- [중급 41] 수익률이 로그 정규 분포를 따르는 두 자산에 분산 투자하면 어떻게 될까? (완전 독립 관계인 경우)
함께 읽으면 좋은 글 (인기 글)




