지난 글에서 자산의 수익률 분포를 정규 분포로 가정했을 때, 현금과 혼합한 포트폴리오의 특성을 평균-분산 그래프에 나타내 보았습니다. 현금 비중을 늘려 위험 자산의 비중을 낮출수록 기대 수익률도 낮아지지만, 위험이라 할 수 있는 불확실성도 함께 줄어듬을 좀 더 직관적으로 이해할 수 있었습니다. 지난 글: 투자 성과 분석의 초급 - 10. 기대 수익률과 불확실성을 함께 표현해 보자 (평균-분산 그래프)
투자 기간 역시 수익률 분포에 영향을 미칩니다. 정규 분포 모델이라면 투자 기간이 길어질수록 수익률과 표준 편차가 증가합니다. 하지만 큰 수의 법칙 효과에 의해 수익률에 비해 표준 편차는 더디게 증가합니다. 결과적으로 기간 대비 평균 수익률의 표준 편차는 줄어듭니다. 참고: 연평균 수익률이 기간 대비 평균 수익률입니다.
아래는 1년 수익률을 N(10%, 20%²)으로 모델링한 어떤 자산의 최대 20년간 투자 수익률의 분포입니다. 수익률 분포는 간결하게 10%, 50%(중앙값), 90% 분위수로 표시했습니다. 1년 평균 수익률은 10%이며, 1년 수익률의 표준 편차는 20%입니다. 출처: 투자 성과 분석의 초급 - 7. 정규 분포에서 표준 편차가 변하면 장기 투자에 어떤 현상이 발생할까?

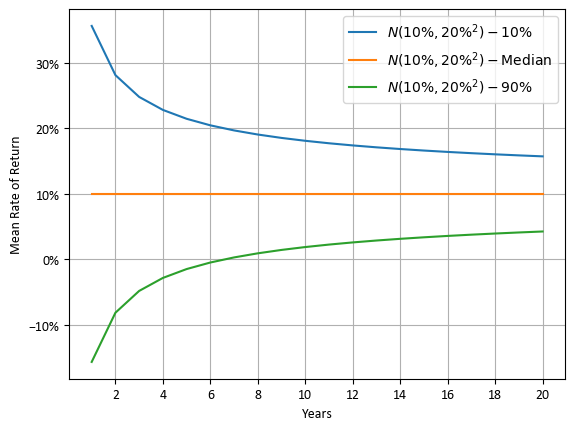
왼쪽 그래프는 누적 수익률을, 오른쪽 그래프는 (기간 대비) 평균 수익률을 보여주고 있습니다. 오른쪽 그래프를 보면 큰 수의 법칙 효과로 평균 수익률의 분포가 점점 밀집됨을 알 수 있습니다. 참고: 설명과 이해의 편의를 위해 매년 동일한 금액을 투자하는 단리 투자를 가정합니다.
이 두 그래프는 3가지 변수가 있습니다. x축은 투자 기간이고, y축은 수익률입니다. 그래프에서 [10%, 90%] 구간은 평균 대비 ±1.28 표준 편차 구간에 해당됩니다. 투자 기간이 길어지면 표준 편차가 평균 대비 줄어드는 것을 볼 수 있습니다.
이 두 그래프를 이전 글에서 살펴보면 평균-분산 그래프로 다시 그려보면 어떤 모양이 될까요?
공지: 책 출간으로 인해 부분 공개로 전환합니다. 보다 이해하기 쉽게 수정 보완한 책을 참고하시기 바랍니다. 양해 부탁드립니다. 책 소개: 왜 위험한 주식에 투자하라는 걸까? (장기 투자와 분산 투자에 대한 통계학적 시각) 출간에 부쳐 (샘플북 포함)

주의: 이 글은 특정 상품 또는 특정 전략에 대한 추천의 의도가 없습니다. 이 글에서 제시하는 수치는 과거에 그랬다는 기록이지, 앞으로도 그럴 거라는 예상이 아닙니다. 분석 대상, 기간, 방법에 따라 전혀 다른 결과가 나올 수 있습니다. 데이터 수집, 가공, 해석 단계에서 의도하지 않은 오류가 있을 수 있습니다. 일부 설명은 편의상 현재형으로 기술하지만, 데이터 분석에 대한 설명은 모두 과거형으로 이해해야 합니다.
투자 기간에 따른 수익률 분포의 변화
(책 출간으로 내용 생략)

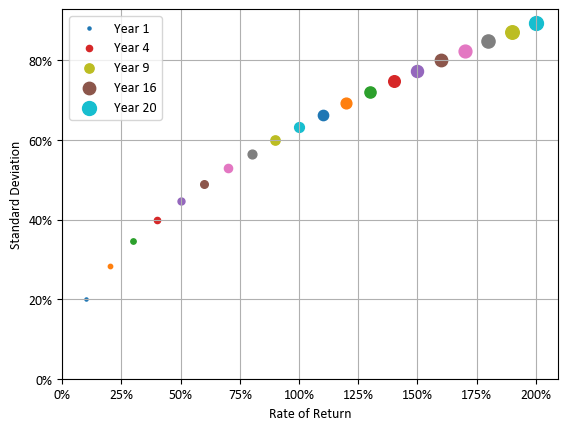
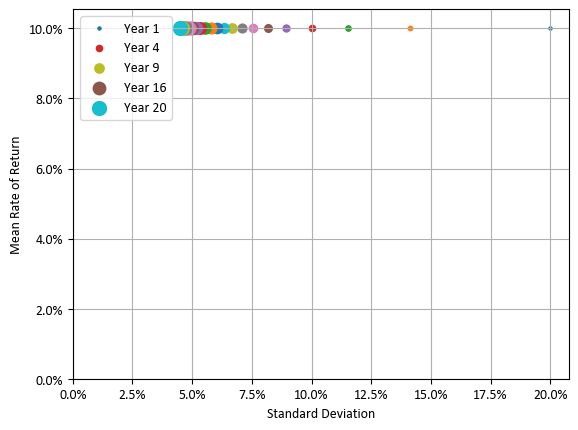
![평균 수익률과 표준편차 (간략화한 상자 수염 그림 [75%, 95%])](https://blog.kakaocdn.net/dna/DImjV/btsKz4jxZ1N/AAAAAAAAAAAAAAAAAAAAAC4YlHTYgun3NnFQiobjvDn9zlBZMWuygqvhh8N81iWg/img.png?credential=yqXZFxpELC7KVnFOS48ylbz2pIh7yKj8&expires=1767193199&allow_ip=&allow_referer=&signature=Vu7wtd0m7lBDMeRG77UrrBi5jdI%3D)
정리하며
투자 기간이 길어지면, 자산의 수익률과 표준 편차(불확실성 또는 위험) 모두 증가합니다. 자산의 수익률 증가에 비해 표준 편차의 증가는 더딥니다. 누적 수익률은 투자 기간에 선형으로 증가하지만, 표준 편차는 투자 기간의 제급근에 비례해서 커지기 때문입니다.
이러한 특성으로 인해 기간 대비 평균 수익률로 보면 표준 편차가 점차 감소하여 기대 수익률로 수렴하는 큰 수의 법칙 현상이 나타납니다. 현실적인 중장기 투자 기간이라 할 수 있는 4년과 16년은 표준 편차를 각각 1 / 2과 1 / 4로 줄여줄 수 있습니다.
이어지는 글: 투자 성과 분석의 초급 - 12. 다시 보자! 샤프 비율 (투자 기간과 투자 비중에 따른 기대 수익률과 불확실성을 평균-분산 그래프에 나타내 보자)
목차: [연재글 목차] 투자 성과 분석 (기초편, 초급편): 순서대로 차근차근 읽으면 좀 더 이해가 쉽습니다.
책 출간 안내: 연재를 정리하여 수정 보완한 <왜 위험한 주식에 투자하라는 걸까? (장기 투자와 분산 투자에 대한 통계학적 시각)>이 출간되었습니다. 종이책(교보문고), 전자책(Yes24, 알라딘, 교보문고, 리디북스)
함께 읽으면 좋은 글:
- 투자 성과 분석의 초급 - 10. 투자 비중에 따른 기대 수익률과 불확실성의 변화를 살펴보자 (평균-분산 그래프)
- 투자 성과 분석의 초급 - 9. 불확실성을 높여 보자 (레버리지 투자, 위험이 증폭되네? 안정적인 레버리지 투자를 위한 기본 요건)
- 투자 성과 분석의 초급 - 8. 불확실성을 낮춰 보자 (현금과의 혼합, 장기 투자에서 왜 예금은 중요하지 않을까?)
- 투자 성과 분석의 초급 - 7. 정규 분포에서 표준 편차가 변하면 장기 투자에 어떤 현상이 발생할까?
- 투자 성과 분석의 초급 - 6. 정규 분포로 보는 큰 수의 법칙 (S&P 500 지수의 수익률 분포는 정규 분포와 유사할까?)
- S&P 500 국내 ETF는 무엇이 좋을까? (국내 상장 ETF 9종 비교와 분석)
- QQQ5(QQQ 5배 레버리지)는 1년간 얼마나 녹았을까?
- JEPI/JEPQ는 특별한가? (SCHD/QQQ + 현금과의 비교)
- 외화 RP는 위험한가? (증권사가 RP를 운용하는 방법)
- 해외 ETF는 세금이 어떻게 부과될까? (배당소득세와 양도소득세)
'주식투자' 카테고리의 다른 글
| [연재글 목차] 투자 성과 분석 (기초편, 초급편, 중급편) (0) | 2024.11.10 |
|---|---|
| 자산을 혼합하면 어떻게 될까? (불확실성이 감소할 수 있다고?) [초급 14] (0) | 2024.11.09 |
| 장기 투자에서의 위험의 변화를 쉽게 표현하고 비교하는 방법은 무엇일까? [초급 13] (0) | 2024.11.08 |
| 다시 보자! 샤프 비율! (투자 기간과 투자 비중에 따른 기대 수익률과 불확실성을 평균-분산 그래프에 나타내 보자.) [초급 12] (0) | 2024.11.08 |
| 평균-분산 그래프 (투자 비중에 따른 기대 수익률과 불확실성의 변화를 나타내 보자) [초급 10] (0) | 2024.11.07 |
| 레버리지 투자 - 수익률을 높여 보자! 위험이 증폭되네? (안정적인 레버리지 투자를 위한 기본 요건) [초급 9] (0) | 2024.11.06 |
| 장기 투자에서 왜 예금은 중요하지 않을까? (불확실성을 낮춰 보자 - 현금과의 혼합) [초급 8] (0) | 2024.11.05 |
| 정규 분포에서 표준 편차가 변하면 장기 투자에 어떤 현상이 발생할까? [초급 7] (0) | 2024.11.05 |




