[초급 16] 서로 독립이면 혼합 포트폴리오는 어떤 형태가 될까? (독립이 아니면 어떻게 될까?)

두 자산의 수익률 방향이 완전히 일치하거나 완전히 반대인 경우 평균-분산 그래프에서 혼합 포트폴리오가 어디에 위치하는지 이전 글에서 살펴보았습니다. 두 경우를 조합하면 삼각형 형태가 만들어집니다. 현실의 자산은 대개 두 가지 극단적 상황의 사이에 있습니다. 그중에서 두 자산의 수익률이 서로 아무런 관계가 없는 경우를 서로 독립(independent)이라고 합니다. 독립인 경우 혼합 포트폴리오는 어떤 형태가 되는지 살펴봅니다. 지난 글: 투자 성과 분석의 초급 - 15. 혼합 포트폴리오의 수익률과 표준 편차의 범위는 어떻게 될까? (삼각형을 그려보자!)

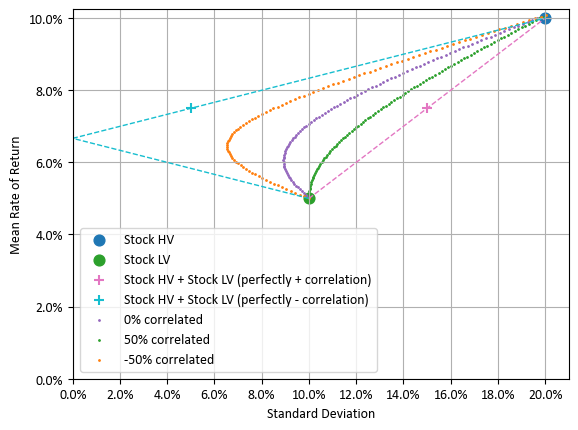
고변동 주식과 저변동 주식의 수익률 분포가 각각 N(10%, 20%²)와 N(5%, 10%²)을 따른다고 하겠습니다. 고변동 주식은 기대 수익률이 높은 대신 변동성(불확실성)이 높고, 저변동 주식은 기대 수익률이 낮은 대신 변동성도 낮습니다.

두 자산에 분산 투자하는 혼합 포트폴리오의 위치는 아래와 같이 평균-분산 그래프에 나타낼 수 있습니다.

두 자산을 혼합하여 만들 수 있는 포트폴리오의 범위

모든 가능한 포트폴리오는 점선으로 만들어진 삼각형의 선분 위 또는 내부에 위치하게 됩니다. 두 자산이 서로 독립이라면 어떻게 될까요?

주의: 이 글은 특정 상품 또는 특정 전략에 대한 추천의 의도가 없습니다. 이 글에서 제시하는 수치는 과거에 그랬다는 기록이지, 앞으로도 그럴 거라는 예상이 아닙니다. 분석 대상, 기간, 방법에 따라 전혀 다른 결과가 나올 수 있습니다. 데이터 수집, 가공, 해석 단계에서 의도하지 않은 오류가 있을 수 있습니다. 일부 설명은 편의상 현재형으로 기술하지만, 데이터 분석에 대한 설명은 모두 과거형으로 이해해야 합니다.

서로 독립인 두 자산의 평균 수익률과 표준 편차

수익률이 정규 분포를 따르면서 서로 독립인 두 자산을 혼합하면 혼합 포트폴리오도 정규 분포를 따른다고 설명하였습니다. 정규 분포는 서로 독립인 경우 더하기 연산에 대해 닫혀있기 때문입니다. 참고: 투자 성과 분석의 초급 - 4. 왜 수익률 모델로 정규 분포를 사용할까?

N(10%, 20%²)에 비중 a로 투자하고, N(5%, 10%²)에 비중 (1 - a)로 투자하는 혼합 포트폴리오의 평균과 분산(variance)은 아래와 같이 계산할 수 있습니다.

평균 = 10% × a + 5% × (1 - a) = 5% × a + 5%

분산 = 20%² × a² + 10%² (1 - a)² = 4%a²  + 1%(1 - a)² = 4%a² + 1% - 2%a + 1%a² = 5%a² - 2%a + 1%

표준 편차는 분산의 양의 제곱근이기에 아래와 같이 됩니다.

표준 편차 = √(5%a² - 2%a + 1%)

이전까지는 깔끔하게 a에 대한 1차 선형식으로 나타났지만, 이번에는 2차식이 되었습니다. 유도한 평균 및 표준 편차 수식을 이용하여 평균-분산 그래프에 그려보면 아래와 같은 형태가 됩니다.

서로 독립인 두 자산을 혼합했을 때 얻을 수 있는 평균 수익률과 표준 편차

서로 독립인 두 자산을 혼합한 보라색 포트폴리오는 삼각형 내부에 위치합니다. 형태는 곡선이며 마치 하늘색 선과 핑크색 선이 서로 끌어당기는 듯한 형상이 됩니다.

표준 편차가 이동한 정도는 두 자산의 투자 비중에 따른 산술 평균이 아닙니다. 자세히 보면 하늘색 선의 표준 편차가 최소가 되는 수익률 위치 6.66%보다 조금 낮은 6% 수익률 위치에서 보라색 점의 표준 편차가 최소가 됩니다.

보라색 혼합 포트폴리오의 표준 편차가 최소화되는 지점은 분산(표준 편차의 제곱)과 관련이 있습니다. 표준 편차의 비는 10% : 20% = 1 : 2이고, 분산의 비는 10%² : 20%² = 1 : 4입니다. 보라색 혼합 포트폴리오의 표준 편차는 두 자산의 수익률 간격이 1 : 4 거리에서 최소가 됩니다. 참고: 분산을 a에 대해 미분하면 계산할 수 있습니다. 분산을 미분하고 최소 지점을 구하면 10%a - 2% = 0이니 a = 0.2가 됩니다. a : (1 - a) = 20% : 80% = 1 : 4인 지점입니다.

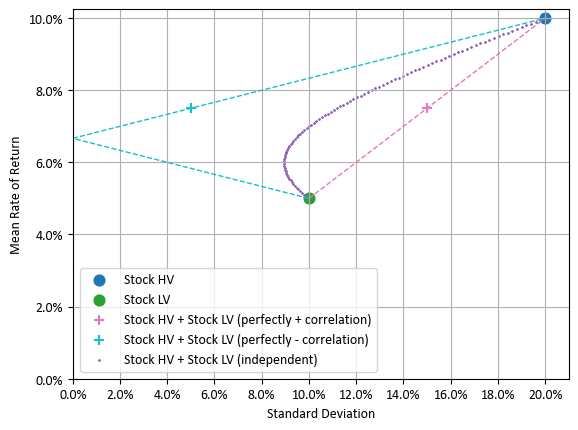
서로 독립이 아니면 어떻게 될까?

현실의 자산은 대개 서로 독립이 아닙니다. 두 자산의 수익률이 일부 비슷하게 움직이거나, 일부 엇갈려서 움직인다면 혼합 포트폴리오는 어떻게 변할까요? 참고: 현금 또는 예금은 변동성이 없다고 가정할 경우 독립이 됩니다.

아래는 두 자산이 50% 같은 방향으로 일치하거나, 50% 다른 방향으로 움직이는 경우를 나타낸 그래프입니다. 참고: 50%는 독립이고, 나머지 50%의 방향 일치 여부를 말합니다.

부분적으로 상관성이 있을 경우 포트폴리오의 이동

가운데 보라색 선은 두 자산이 독립으로 상관성이 없는 경우입니다. 오른쪽 초록색 선은 두 자산 간 수익률이 50%는 독립이고, 나머지 50%는 일치하는 경우입니다. 왼쪽 오렌지색 선은 두 자산 간 수익률이 50%는 독립이고, 나머지 50%는 반대 방향인 경우입니다.

두 자산의 수익률이 비슷하게 움직일수록 오른쪽으로, 두 자산이 엇갈리게 움직일수록 왼쪽으로 이동합니다. 50%와 -50%는 두 분포의 선형 상관성을 추정한 피어슨 상관 계수와 동일한 값입니다.

정리하며

평균-분산 그래프에서 두 자산으로 만들 수 있는 포트폴리오의 위치는 모든 가능한 상관성을 고려하면 삼각형이 됩니다. 두 자산의 상관성이 주어지면, 삼각형 내 두 자산을 연결하는 곡선으로 제한됩니다. 다르게 말하면, 상관성에 따라 만들어질 수 있는 모든 곡선이 모여 삼각형이 된 것입니다.

두 자산의 수익률 분포가 서로 독립인 경우 포트폴리오의 위치는 삼각형을 가로지르는 곡선이 됩니다. 두 자산의 수익률 관계가 독립보다 조금 더 유사한 경향이면, 곡선은 오른쪽으로 이동하며, 독립보다 좀 더 어긋나는 경향이면, 곡선은 왼쪽으로 이동합니다.

흥미로운 현상입니다. 그런데 투자에는 어떻게 활용할 수 있는 것일까요?

이어지는 글: [초급 17] 평균-분산 그래프에서 우위 관계 (내가 더 나아! 아니야! 불확실해!)

목차: [연재글 목차] 투자 성과 분석 (기초편, 초급편): 순서대로 차근차근 읽으면 좀 더 이해가 쉽습니다.

책 안내: 연재를 정리하여 수정 보완한 <왜 위험한 주식에 투자하라는 걸까? (장기 투자와 분산 투자에 대한 통계학적 시각)>이 출간되었습니다. 종이책(교보문고), 전자책(Yes24, 알라딘)

함께 읽으면 좋은 글:

• [초급 15] 혼합 포트폴리오의 수익률과 표준 편차의 범위는? (삼각형을 그려보자!)
• [초급 14] 자산을 혼합하면 어떻게 될까? (불확실성이 감소할 수 있다고?)
• [초급 13] 장기 투자에서의 위험의 변화를 쉽게 표현하고 비교하는 방법은 무엇일까?
• [초급 12] 다시 보자! 샤프 비율! (투자 기간과 투자 비중에 따른 기대 수익률과 불확실성을 평균-분산 그래프에 나타내 보자.)
• [초급 11] 투자 기간에 따른 기대 수익률과 불확실성의 변화를 평균-분산 그래프에 나타내 보자.
• S&P 500 국내 ETF는 무엇이 좋을까? (국내 상장 ETF 9종 비교와 분석)
• QQQ5(QQQ 5배 레버리지)는 1년간 얼마나 녹았을까?
• JEPI/JEPQ는 특별한가? (SCHD/QQQ + 현금과의 비교)
• 해외 ETF는 세금이 어떻게 부과될까? (배당소득세와 양도소득세)
• 외화 RP는 위험한가? (증권사가 RP를 운용하는 방법)