[데이터 분석 6] 수익률 분포를 정규 분포로 모델링하고 위험을 추정해 보자 (구글 시트 편)

이전 글에서 SPY의 1년 수익률 분포를 정규 분포와 비교해 보았습니다. SPY 수익률 분포는 정규 분포와 비슷한 면도 있었고, 그렇지 않은 점도 있었습니다. SPY 수익률 분포는 정규 분포에 비해 중앙에 분포가 더 밀집되어 있었고, 큰 손실이 발생하는 빈도는 정규 분포에 비해 높았습니다. 이전 글: [데이터 분석 5] 수익률 분포를 정규 분포와 함께 그려보자 (구글 시트 편)

자산의 수익률 분포는 정규 분포와 다른 점이 꽤 있지만, 정규 분포는 현실적으로 손쉽게 분석에 사용할 수 있는 유용한 방법 중에 하나입니다. 투자자는 정규 분포를 가정하여 분석한 결과는 기반이 되는 과거 데이터와 다를 수 있으며, 경우에 따라서는 위험이 과소 평가될 수도 있음을 감안하고 참고하여야 합니다. 참고: [초급 4] 투자에서 수익률 모델로 왜 정규 분포를 사용할까?

자산의 수익률 분포를 정규 분포로, 매년 수익률 분포가 서로 독립이라 가정했을 때, 장기 투자를 하면 위험이 어떻게 변하는지 그래프로 그려봅니다. 참고: [초급 13] 장기 투자에서의 위험의 변화를 쉽게 표현하고 비교하는 방법은 무엇일까?

참고: 이 연재는 책 <왜 위험한 주식에 투자하라는 걸까? - 장기 투자와 분산 투자에 대한 통계학적 시각>에서 소개한 주요 분석 방법을 구글 시트로 적용해 보는 부록의 성격을 가집니다. 책의 초고에 해당되는 블로그 글이나 읽기 편하게 정리하고 편집한 책을 한두 번 차근차근 읽어 분석 방법의 의미를 이해한 후에 보면 더욱 좋습니다. 연재 그 자체만으로도 따라 하기에 별 무리가 없는 수준으로 설명하려고 하지만, 세부적인 설명이 일부 생략되어 있을 수 있고, 분석 방법을 이해한 상태에서 보면 좀 더 도움이 될 수 있기 때문입니다.

주의: 이 글은 특정 상품 또는 특정 전략에 대한 추천의 의도가 없습니다. 이 글에서 제시하는 수치는 과거에 그랬다는 기록이지, 앞으로도 그럴 거라는 예상이 아닙니다. 분석 대상, 기간, 방법에 따라 전혀 다른 결과가 나올 수 있습니다. 데이터 수집, 가공, 해석 단계에서 의도하지 않은 오류가 있을 수 있습니다. 일부 설명은 편의상 현재형으로 기술하지만, 데이터 분석에 대한 설명은 모두 과거형으로 이해해야 합니다.

SPY에 장기 투자했을 때의 수익률 분포 추정

이전 글에서 살펴본 SPY의 1년(250거래일) 평균 수익률은 11.7%였고, 표준 편차는 16.9%였습니다. 정규 분포로 모델링하면 N(11.7%, 16.9%²)으로 표현할 수 있습니다. 다음 그림에서 왼쪽은 표준 편차를 계산하는 수식을 보여주는 구글 시트이고, 오른쪽은 SPY 수익률 분포를 정규 분포와 함께 표시한 그림입니다.

SPY의 1년(250거래일) 수익률에 대한 평균과 표준 편차 및 정규 분포 모델

매년 수익률이 정규 분포를 따르고, 수익률 분포가 서로 독립이라면, k년 투자 시 수익률은 평균과 분산 모두 k배가 됩니다. 표준 편차는 분산의 양의 제곱근이니 √k배가 됩니다. 참고: [초급 7] 정규 분포에서 표준 편차가 변하면 장기 투자에 어떤 현상이 발생할까?

k × N(μ, σ²) = N(kμ, kσ²)

이제 SPY 투자 기간에 따른 수익률의 정규 분포도 추정할 수 있습니다. SPY의 과거 데이터를 요약하여 1년 수익률 분포가 정규 분포를 따른다는 가정하에서 분석하는 것입니다. 실제와 상당히 다를 수 있으며, 실제와 유사하더라도 이는 동일한 데이터에 기반해서 통계량을 추출했기 때문에 자연스러운 현상입니다. 참고: [초급 부록 A3] 레버리지 ETF는 기초 자산(본주)보다 얼마나 위험할까? (SPY vs SSO = SPY ×2)

SPY의 1년 수익률과 표준 편차를 참조로 가져오고, 투자 기간에 따른 평균과 표준 편차를 계산합니다. 1년 평균 수익률은 k배로, 표준 편차는 √k배를 하면 됩니다. SQRT() 함수를 사용할 수 있습니다.

정규 분포로 모델링한 SPY의 투자 기간별 평균 수익률과 표준 편차

그림에서 투자 기간(Years) 옆에 있는 평균(Mean)은 말 그대로 평균입니다. 정규 분포를 가정했기에 좌우대칭으로 수익률이 분포하기에 평균은 중앙값이 됩니다. 101명이 투자했다면 수익률 순위 51등에 해당되는 투자자가 얻게 되는 수익률이라 볼 수 있습니다.

대개의 투자자가 관심을 가지는 것은 위험입니다. SPY의 장기 수익률이 높을 거라 기대하지만, 운이 나쁘면 손실이 얼마나 날지가 궁금할 수 있습니다. 정규 분포에서 특정 누적 확률에 해당하는 값을 구하는 함수는 NORMINV()  함수입니다. 이 함수를 이용하면, 다음의 왼쪽 그림과 같이 하위 25%와 하위 5%에 해당하는 수익률을 추정할 수 있습니다.

SPY의 투자 기간에 따른 추정 누적 수익률 (정규 분포 가정)

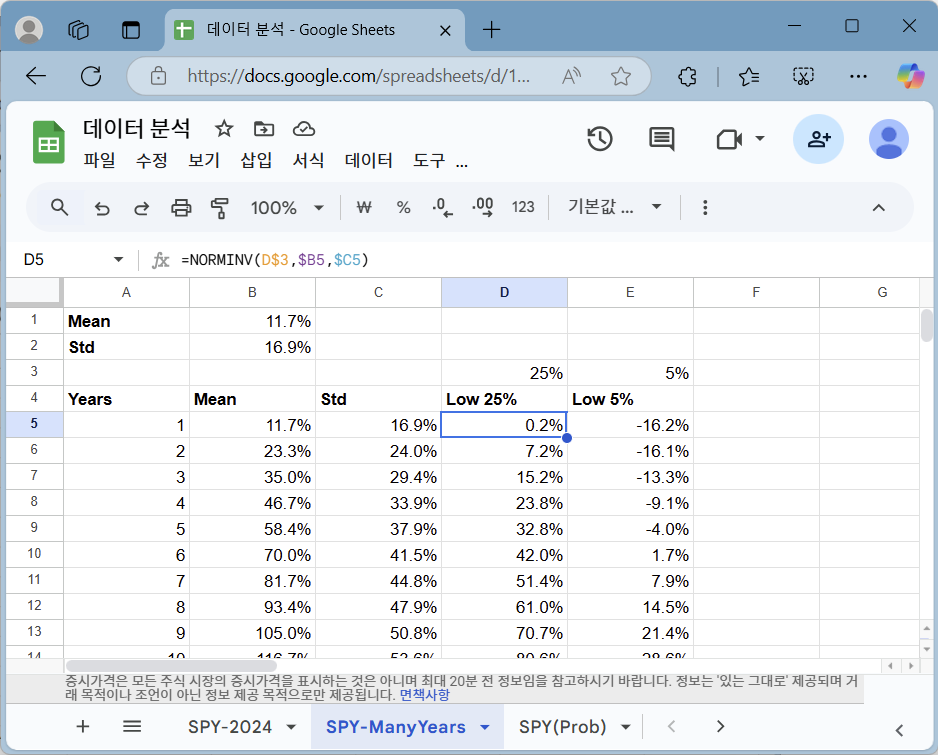
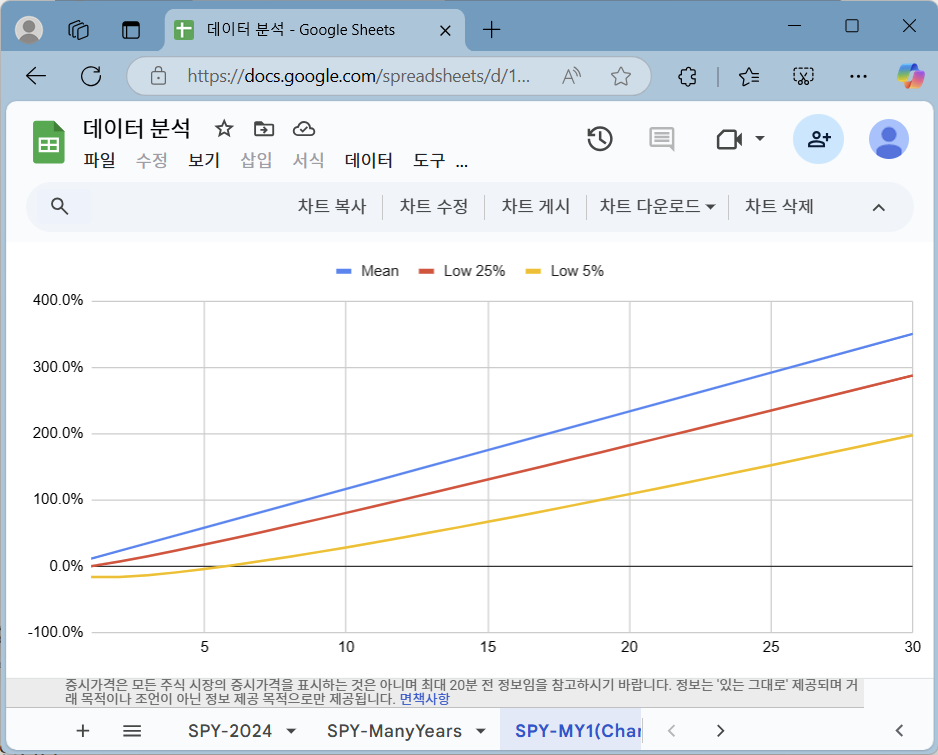
중앙값(Mean, 여기서는 정규 분포이기에 평균이 중앙값이 됩니다), 하위 25%, 하위 5%에 대해 추정한 수익률로 그래프를 그린 결과가 오른쪽 그림입니다.

연평균 수익률로 살펴본 장기 투자 시 수익률 변화

그래프가 그려지기는 하지만 이해하기 어렵습니다. 다음은 누적 수익률을 1년 평균 수익률로 환산해서 다시 그린 그림입니다.

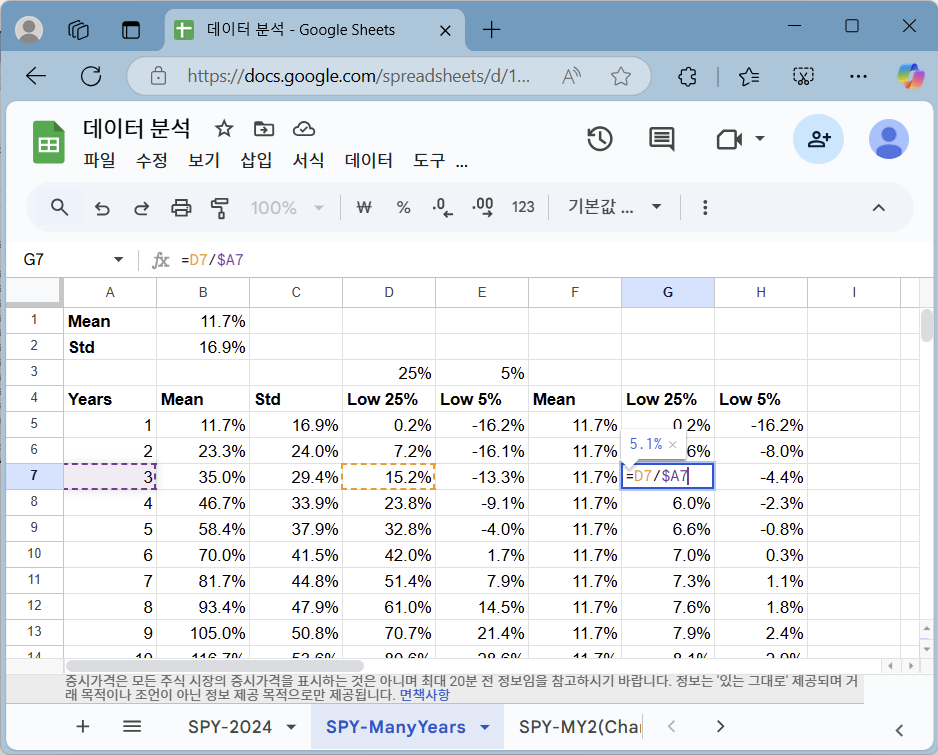
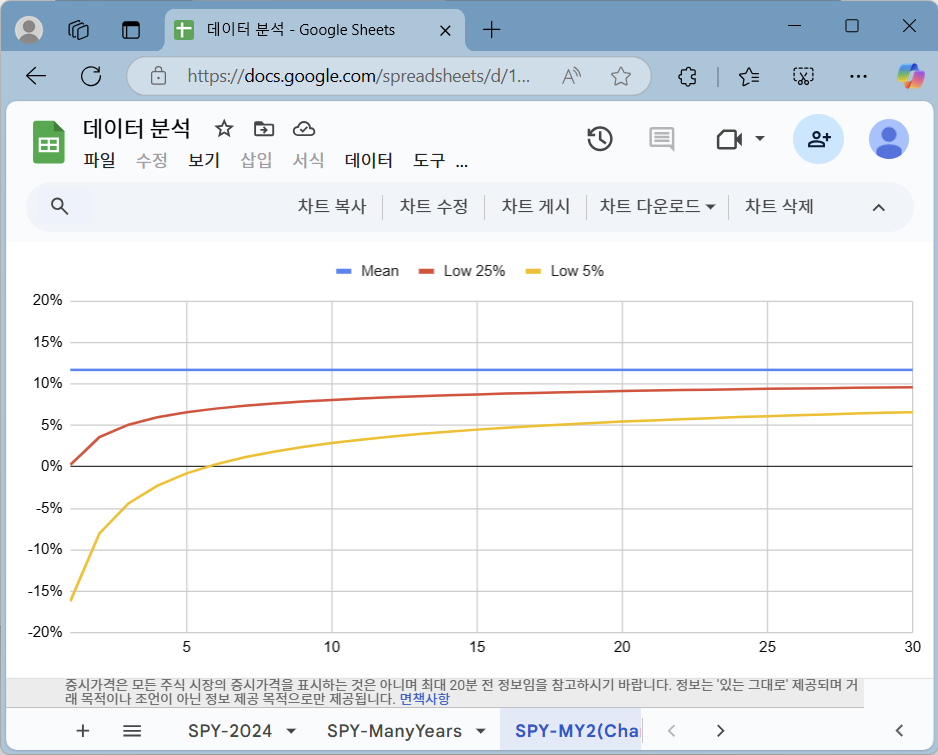
이 그래프는 수익률 대신 자산비를 쓰고 로그 스케일로 그려야 합니다. 구글 시트는 로그 스케일을 적용하면 세부 설정에 제약이 많아 분석에 사용하기 어려워지게 산술 스케일을 사용했습니다. 오른쪽 그래프는 y축 최소값과 최대값을 각각 -20%(-0.2)와 20%(0.2)로 설정하고, 세로축 눈금이 5% 단위로 나타나도록 세로 격자선 개수를 9개로 설정한 결과입니다.

이제 대략적인 위험을 추정해 볼 수 있습니다. 하위 25% 즉 75% 확률로 1년 투자 시 손실이 발생하지 않았다고 추정되었습니다. 운이 나쁜 하위 5% 순위의 투자자의 경우 대략 6년간 투자했다면, 원금 손실이 사라졌다고 추정되었습니다. 다르게 말하면 6년간 투자하면 95% 확률로 원금 손실이 없어졌다고 볼 수 있습니다.

그래프에서 볼 수 있는 장기 투자 시 1년 평균 수익률이 모두 수렴하는 큰 수의 법칙 현상이 나타납니다. 이는 수익률 분포를 서로 독립인 정규 분포로 가정했기 때문에 자연스러운 현상입니다. 참고: [기초 15 마지막 편] 장기 투자는 왜 위험이 줄어드는가? (불확실성이 누적될수록 확실해진다고?)

주의: SPY의 과거 수익률 분포를 정규 분포로 모델링해서 쉽게 이해할 수 있도록 표현하고 해석하는 것입니다. 미래에 대한 예측이 아닙니다. 모든 통계량은 과거 데이터를 요약한 값입니다.

예금과의 비교

투자자가 3% 이자를 받을 수 있는 예금에도 가입할 수 있다고 했을 때, 예금과의 함께 비교해 볼 수 있습니다.

SPY 수익률과 예금의 비교 (SPY 수익률은 정규 분포로 모델링)

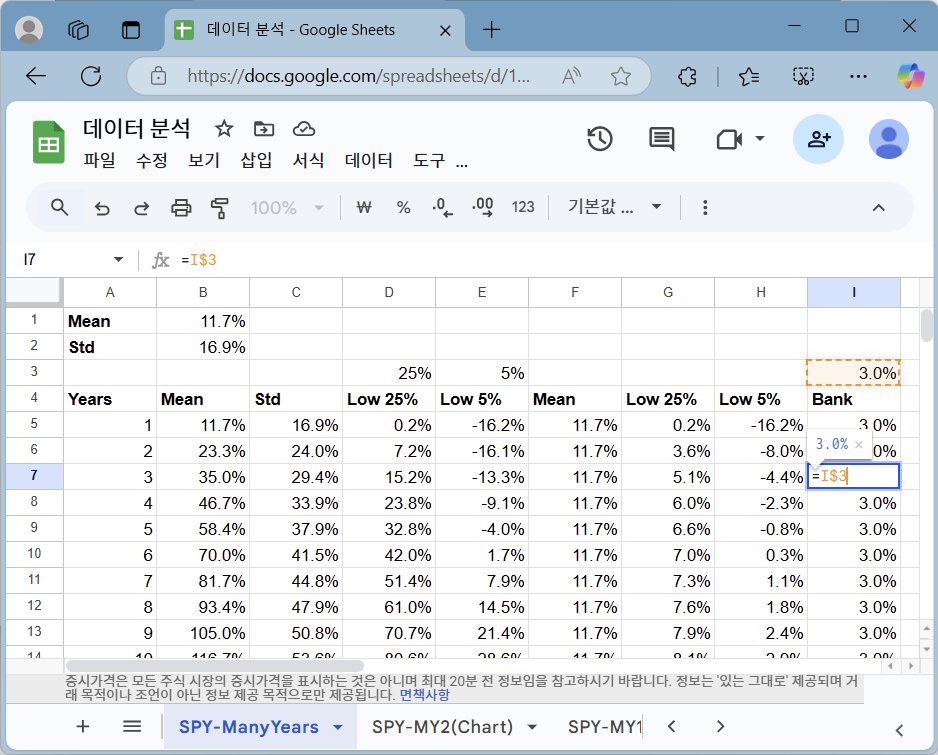
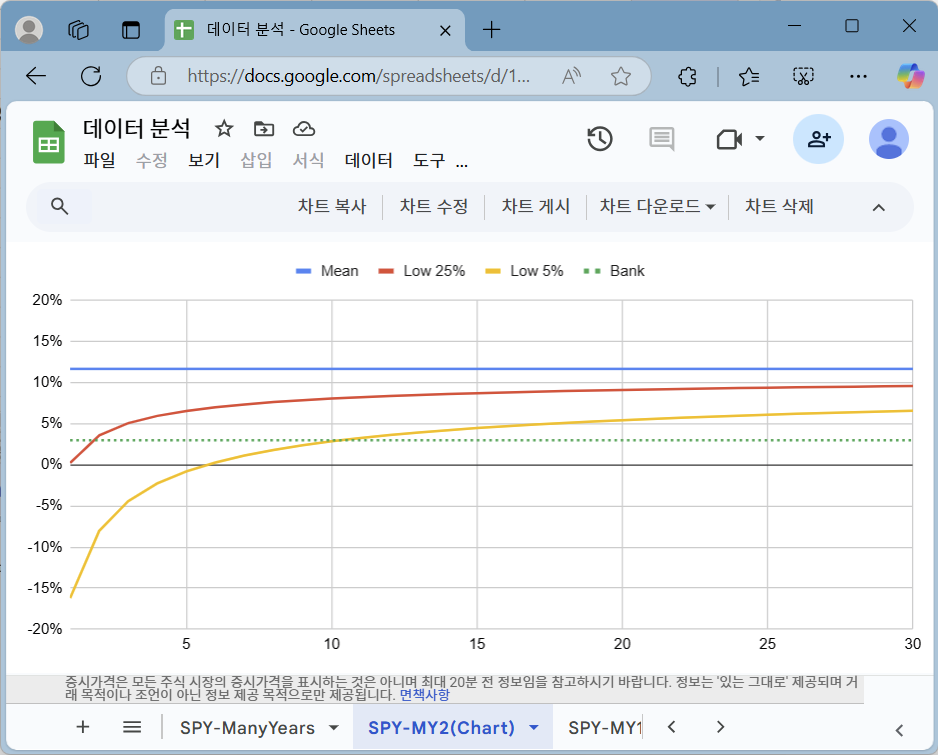
왼쪽은 연평균 수익률이 3%인 예금을 정의한 것이고, 오른쪽을 예금을 그래프에 함께 나타낸 것입니다. SPY에 대략 10년 정도 투자하면 95% 확률로 예금보다 나은 성과를 얻을 수 있었다고 추정되었습니다.

참고: 이 연재에서는 단리 투자를 가정하고 분석합니다. 이후 평균-분산 그래프를 이용한 분석에서 선형적으로 쉽게 해석하기 위해서입니다. 현실에서 투자자는 복리 투자를 할 가능성이 높기에 분석 결과와 다소 차이가 발생할 수 있습니다. 하지만 대략적인 경향을 파악하는 데는 큰 무리가 없습니다.

정리하며

SPY의 1년 수익률 분포를 정규 분포로 가정하고, 장기 투자에서의 위험 감소 경향을 살펴보았습니다. 6년 정도 투자했다면 원금 손실 가능성이 5% 정도가 되었던 것으로 추정되었습니다. 3% 금리를 주는 예금도 함께 그래프에 나타내어 비교해 보니, 예금보다 높은 수익률을 얻을 가능성이 95% 이상이 되려면 10년 정도 투자했어야 했습니다.

이어지는 글: [데이터 분석 7] 자산과 예금의 혼합을 평균-분산 그래프에 나타내 보자 (구글 시트 편)

목록: 자산 배분 분석 방법과 사례 글 모음 [목록] (순서대로 차근차근 읽기를 권합니다)

함께 읽으면 좋은 글:

• [데이터 분석 5] 수익률 분포를 정규 분포와 함께 그려보자 (구글 시트 편)
• [데이터 분석 4] 주가 데이터에서 위험 지표인 MDD를 뽑아보자 (구글 시트 편)
• [데이터 분석 3] 주가 데이터에서 수익률 통계량을 뽑아보자 (구글 시트 편)
• [데이터 분석 2] TR 데이터를 받아 그래프로 그려보자 (구글 시트 편)
• [데이터 분석 1] 주가 데이터를 불러와서 그래프로 그려보자 (구글 시트 편)
• S&P 500 국내 ETF는 무엇이 좋을까? (국내 상장 ETF 9종 비교와 분석)
• 나스닥 100 국내 ETF는 무엇이 좋을까? (국내 상장 ETF 5종 비교와 분석)
• QQQ5(QQQ 5배 레버리지)는 1년간 얼마나 녹았을까?
• 한국인은 커버드콜 ETF에 장기 투자해도 좋을까? - 커버드콜 ETF에 대한 글 모음
• 외화 RP는 위험한가? (증권사가 RP를 운용하는 방법)