이제 평균-분산(Mean-Variance) 그래프를 이용하여 자산의 성과를 표시하고 비교 분석하는 방법을 소개합니다. 평균-분산 그래프 역시 과거 데이터에 대한 통계량을 그래프로 표현한 것이므로 미래에 대한 예측이 아닙니다. 다만 신뢰할 수 있는 어떤 이유로 인해 미래에도 특정한 경향이 지속될 거라 믿는다면, 투자에 참고할 수 있습니다. 평균-분산 그래프를 어떻게 해석하는지는 평균-분산(Mean-Variance) 그래프 해석 방법 및 주의 사항을 참고하기 바랍니다.

주의: 이 글은 특정 상품 또는 특정 전략에 대한 추천의 의도가 없습니다. 이 글에서 제시하는 수치는 과거에 그랬다는 기록이지, 앞으로도 그럴 거라는 예상이 아닙니다. 분석 대상, 기간, 방법에 따라 전혀 다른 결과가 나올 수 있습니다. 데이터 수집, 가공, 해석 단계에서 의도하지 않은 오류가 있을 수 있습니다. 일부 설명은 편의상 현재형으로 기술하지만, 데이터 분석에 대한 설명은 모두 과거형으로 이해해야 합니다.
평균-분산 그래프에 나타낸 SPY와 TLT
아래 왼쪽 그림은 SPY와 TLT의 TR 데이터를 이용하여 250거래일을 1년으로 가정하고 평균 수익률과 표준 편차를 계산한 결과입니다. 참고: [데이터 분석 5] 수익률 분포를 정규 분포와 함께 그려보자 (구글 시트 편)


계산한 평균과 표준 편차로 분산형 차트(scatter plot)를 그린 결과가 오른쪽 그림입니다. SPY와 TLT를 각각 파란색과 빨간색 점으로 표시했고, 가로축과 세로축의 주눈금 범위와 간격을 적절히 설정했습니다. 참고: 구글 시트에서 분산형 차트를 지정할 때, 행/열 전환을 해야 할 수 있습니다.
평균-분산 그래프 상에서 SPY와 예금 혼합 포트폴리오의 표현
SPY와 예금을 혼합해 보겠습니다. 예금은 변동성이 없는 자산으로 간주할 수 있습니다. 변동성이 없는 자산을 혼합하면, 평균과 표준 편차 모두 주된 자산의 투자 비중에 비례해서 선형적으로 줄어듭니다. 참고: [초급 8] 장기 투자에서 왜 예금은 중요하지 않을까? (불확실성을 낮춰 보자 - 현금과의 혼합)
아래 왼쪽 그림과 같이 예금(Bank)의 평균 수익률(2%)과 표준 편차(0%)를 정의하고, SPY 투자 비중을 2%부터 98%까지 2% 단위로 SPY + 예금 혼합 포트폴리오의 평균과 표준 편차를 계산해서 그래프로 나타내면 오른쪽 그림과 같이 됩니다.


그래프에서 SPY, TLT, 예금에 해당되는 점은 크기와 색상을 다르게 설정하였습니다. SPY에 예금을 혼합하면 평균-분산 그래프에서 직선의 형태로 나타납니다. 예금은 변동성이 없는 자산이기 때문입니다.
빨간색 점으로 표시된 TLT는 SPY + 예금 포트폴리오 선 아래에 위치하고 있습니다. 평균-분산 그래프에서 SPY + 예금은 TLT 대비 우위에 있었다고 말할 수 있습니다.
SPY + 예금 > TLT
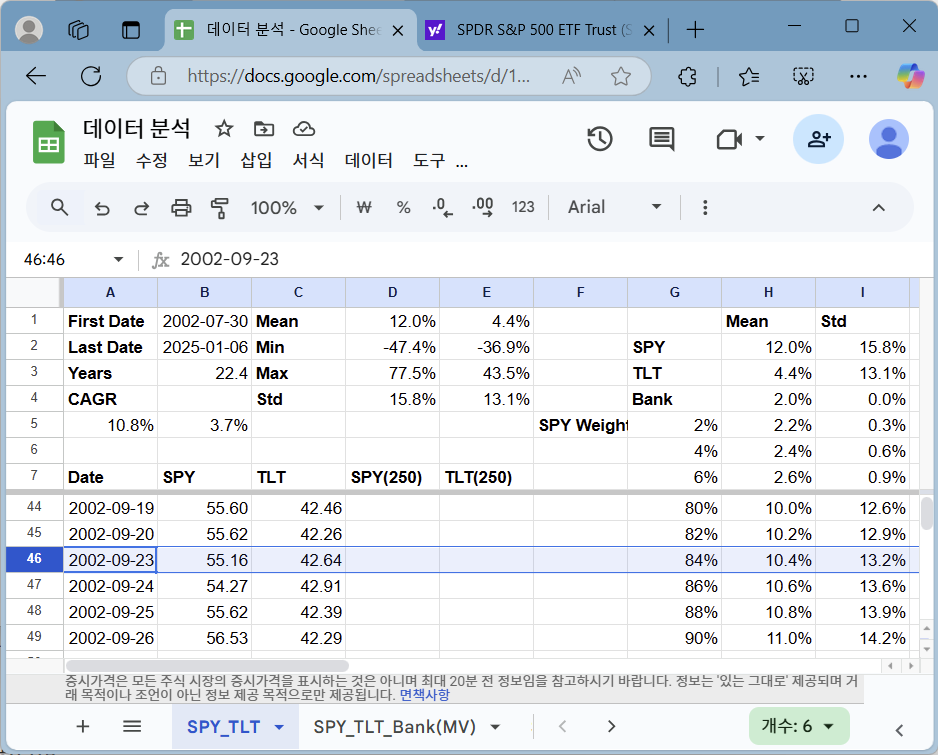
SPY와 예금을 적절히 조합했다면 TLT와 동일한 수준인 13% 정도의 표준 편차로 약 10% 평균 수익률을 얻을 수 있었습니다. 데이터 시트에서 찾아보며 아래 왼쪽 그림과 같이 TLT의 표준 편차와 가장 유사한 지점은 SPY 84% + 예금 16%였습니다. 이때 평균 수익률은 10.4%, 표준 편차는 13.2%였습니다.
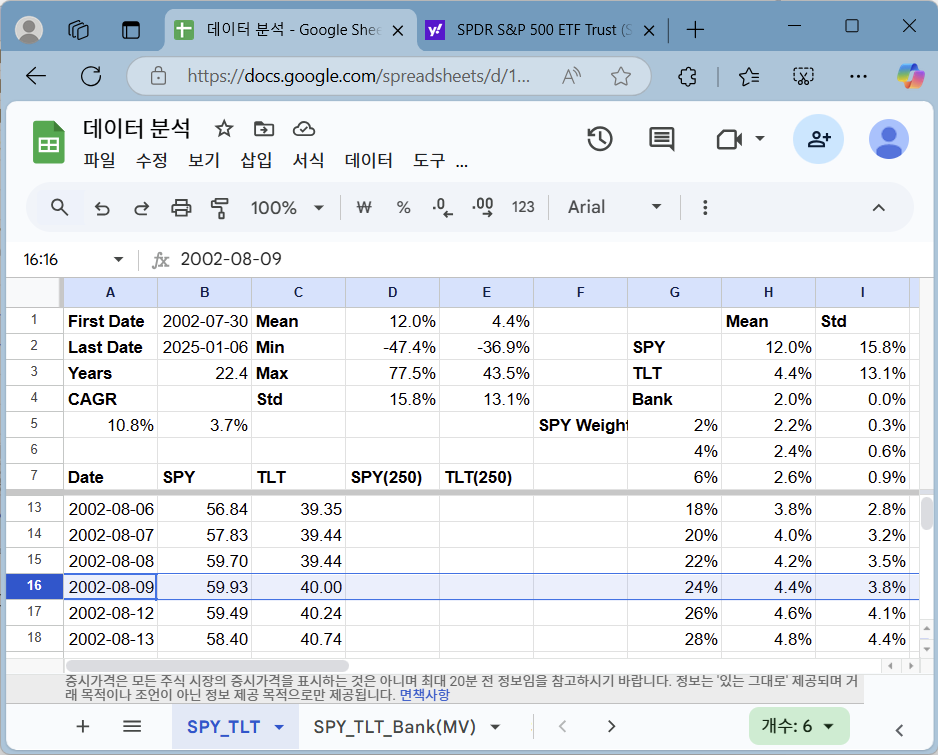
만일 TLT와 비슷한 수익률을 기대했다면, 오른쪽 그림과 같이 SPY 24% + 예금 76% 포트폴리오를 찾을 수 있습니다. 동일한 수준인 4.4% 수익률이었지만, 표준 편차는 3.8%로 TLT의 13.1%의 1 / 3이 되지 않았습니다. 참고: 과거 데이터를 이용하여 특정 조건이 만족되는 포트폴리오를 찾아본 것이지, 과거 투자 시점에 이를 미리 알 수 있었다는 뜻이 아닙니다.
조금 더 파악하기 쉽게 평균-분산 그래프 그리기
앞의 구글 시트에서 작성한 방식으로 만든 평균-분산 그래프는 해석하거나 세밀하게 설정하기 불편합니다. 개별 자산 또는 포트폴리오 종류에 따라 다른 색상이나 크기의 마커(marker)를 설정할 수 없기 때문입니다. 조금 더 편리하게 사용하기 위해서 표준 편차를 x축으로 하고, 평균은 각각의 자산마다 따로 기입하는 방식을 쓸 수 있습니다.
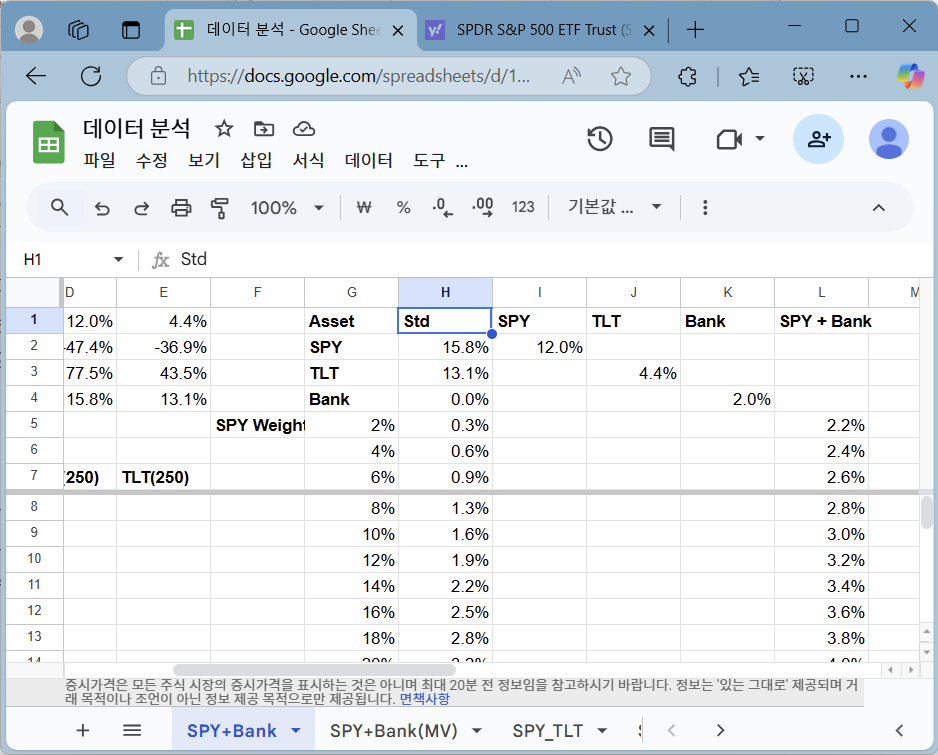
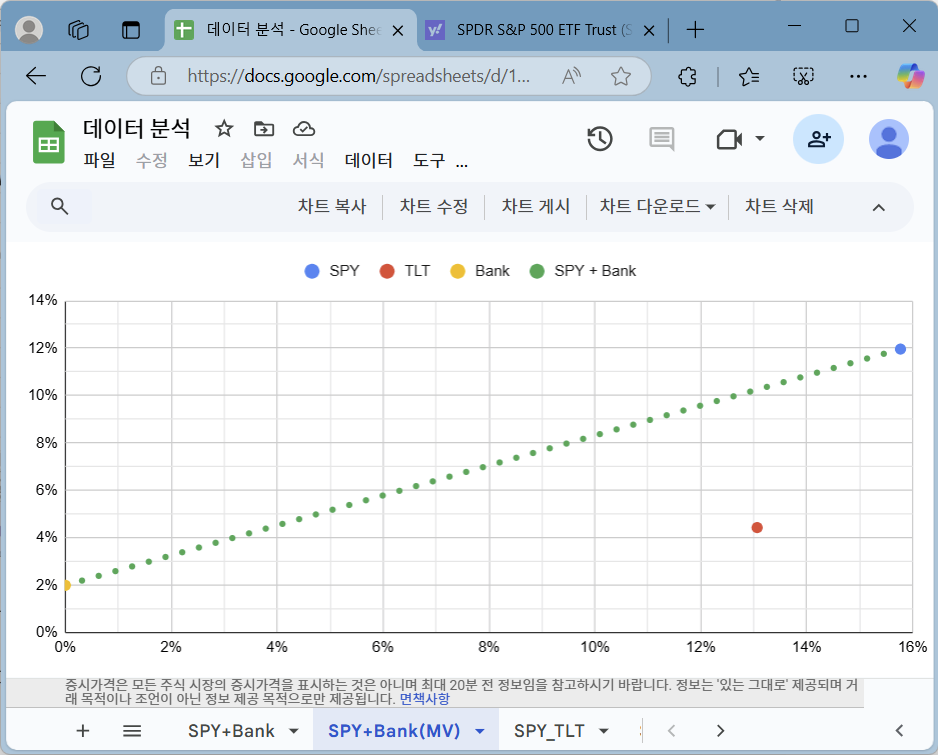
왼쪽 그림은 x축에 해당되는 표준 편차는 공통으로 쓰고, SPY, TLT, 예금(Bank), SPY + 예금(Bank) 각각 따로 칼럼을 두었습니다. 이렇게 데이터를 정돈하고 분산형 차트를 그린 결과가 오른쪽입니다. 범례도 붙기에, 훨씬 이해하기 쉽습니다.
정리하며
SPY와 TLT의 과거 데이터로 평균-분산 그래프에 나타내 보았습니다. SPY + 예금 혼합 포트폴리오는 직선으로 나타나며, 이 직선과 TLT를 비교해 보면, TLT는 SPY + 예금 혼합 포트폴리오 대비 열위에 있었음을 알 수 있었습니다. 혼합 포트폴리오를 그리는 데 사용한 데이터를 살펴보면, TLT와 비슷한 수준의 수익률 또는 유사한 수준의 표준 편차를 가졌던 포트폴리오를 찾을 수 있습니다.
이어지는 글: [데이터 분석 8] 두 자산의 혼합 포트폴리오를 평균-분산 그래프에 나타내 보자 (구글 시트 편)
목록: 자산 배분 분석 방법과 사례 글 모음 [목록] (순서대로 차근차근 읽기를 권합니다)
출간 안내: 연재를 묶어 읽기 쉽게 보완하여 편집한 책이 종이책(교보문고)과 전자책(리디북스, 교보문고, Yes24, 알라딘)으로 출간되었습니다. 책 소개: 구글 시트로 시작하는 투자 포트폴리오 분석 (오렌지사과의 불친절한 워크북) 출간에 부쳐 (샘플북 포함)
참고 서적: <왜 위험한 주식에 투자하라는 걸까? - 장기 투자와 분산 투자에 대한 통계학적 시각> - 이 연재에서 소개하는 각종 분석 방법의 의미를 소개합니다.
함께 읽으면 좋은 글:
- [데이터 분석 6] 수익률 분포를 정규 분포로 모델링하고 위험을 추정해 보자 (구글 시트 편)
- [데이터 분석 5] 수익률 분포를 정규 분포와 함께 그려보자 (구글 시트 편)
- [데이터 분석 4] 주가 데이터에서 위험 지표인 MDD를 뽑아보자 (구글 시트 편)
- [데이터 분석 3] 주가 데이터에서 수익률 통계량을 뽑아보자 (구글 시트 편)
- [데이터 분석 2] TR 데이터를 받아 그래프로 그려보자 (구글 시트 편)
- S&P 500 국내 ETF는 무엇이 좋을까? (국내 상장 ETF 9종 비교와 분석)
- 나스닥 100 국내 ETF는 무엇이 좋을까? (국내 상장 ETF 5종 비교와 분석)
- QQQ5(QQQ 5배 레버리지)는 1년간 얼마나 녹았을까?
- 한국인은 커버드콜 ETF에 장기 투자해도 좋을까? - 커버드콜 ETF에 대한 글 모음
- 외화 RP는 위험한가? (증권사가 RP를 운용하는 방법)
'주식투자' 카테고리의 다른 글
| [데이터 분석 11] 환율을 반영한 환노출 주가를 계산하고 평균-분산 그래프에서 환헤지와 비교해 보자 (구글 시트 편) (1) | 2025.01.09 |
|---|---|
| [데이터 분석 10] 특정 포트폴리오를 평균-분산 그래프에 강조해서 나타내 보자 (구글 시트 편) (0) | 2025.01.08 |
| [데이터 분석 9] 세 자산의 혼합 포트폴리오를 평균-분산 그래프에 나타내 보자 (구글 시트 편) (0) | 2025.01.08 |
| [데이터 분석 8] 두 자산의 혼합 포트폴리오를 평균-분산 그래프에 나타내 보자 (구글 시트 편) (0) | 2025.01.07 |
| [데이터 분석 6] 수익률 분포를 정규 분포로 모델링하여 위험을 추정해 보자 (구글 시트 편) (0) | 2025.01.07 |
| [데이터 분석 5] 수익률 분포를 정규 분포와 함께 그려보자 (구글 시트 편) (0) | 2025.01.06 |
| [데이터 분석 4] 주가 데이터에서 위험 지표인 MDD를 뽑아보자 (구글 시트 편) (1) | 2025.01.06 |
| [데이터 분석 3] 주가 데이터에서 수익률 통계량을 뽑아보자 (구글 시트 편) (2) | 2025.01.06 |




