[데이터 분석 12] 자산과 환율의 시간의 흐름에 따른 상관성 변화를 살펴보자 (구글 시트 편)

자산 배분 또는 분산 투자는 자산 간의 상호 보완 관계를 파악하여 투자 목적에 적절한 개별 자산의 투자 비중을 결정합니다. 모든 통계량이 그러하듯 자산 간의 관계도 시간이 흐름에 따라 변하거나, 일시적으로 장기적인 경향과 다른 양상을 보일 수 있습니다. 참고: [초급 23] 통계량을 예측으로 생각해도 될까? (통계량의 불확실성, 미국 장기 채권 ETF의 수익률 변화)

투자자가 통계량의 장기적인 경향과 일시적인 변동을 나름대로의 합리적인 근거로 구분할 수 있다면, 상황에 따라 적절히 대처를 함으로써 투자 효율을 높일 수 있습니다. 특히 일시적인 큰 변동에 어떻게 대응할 것인지 미리 방안을 세워두면 투자 수익률 또는 안정성을 높일 수도 있습니다. 참고: [초급 24 - 마지막 편] 통계량의 큰 변동은 어떻게 이해해야 할까? (환율의 반란)

이 글에서는 두 자산 수익률 간의 선형적 관계를 파악하는 방법의 하나인 피어슨 상관 계수(Pearson correlation coefficient)를 이용하여 SPY, TLT 및 환율 간의 시간의 흐름에 따른 상관성 변화를 살펴보는 방법을 알아봅니다.

주의: 이 글은 특정 상품 또는 특정 전략에 대한 추천의 의도가 없습니다. 이 글에서 제시하는 수치는 과거에 그랬다는 기록이지, 앞으로도 그럴 거라는 예상이 아닙니다. 분석 대상, 기간, 방법에 따라 전혀 다른 결과가 나올 수 있습니다. 데이터 수집, 가공, 해석 단계에서 의도하지 않은 오류가 있을 수 있습니다. 일부 설명은 편의상 현재형으로 기술하지만, 데이터 분석에 대한 설명은 모두 과거형으로 이해해야 합니다.

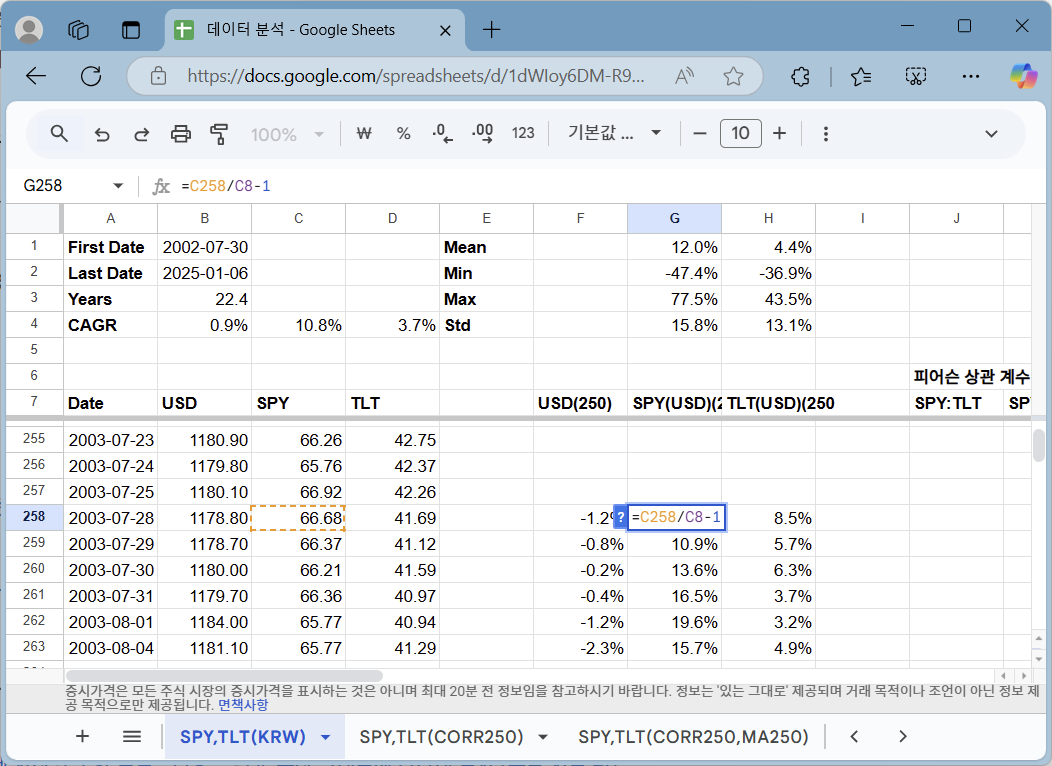
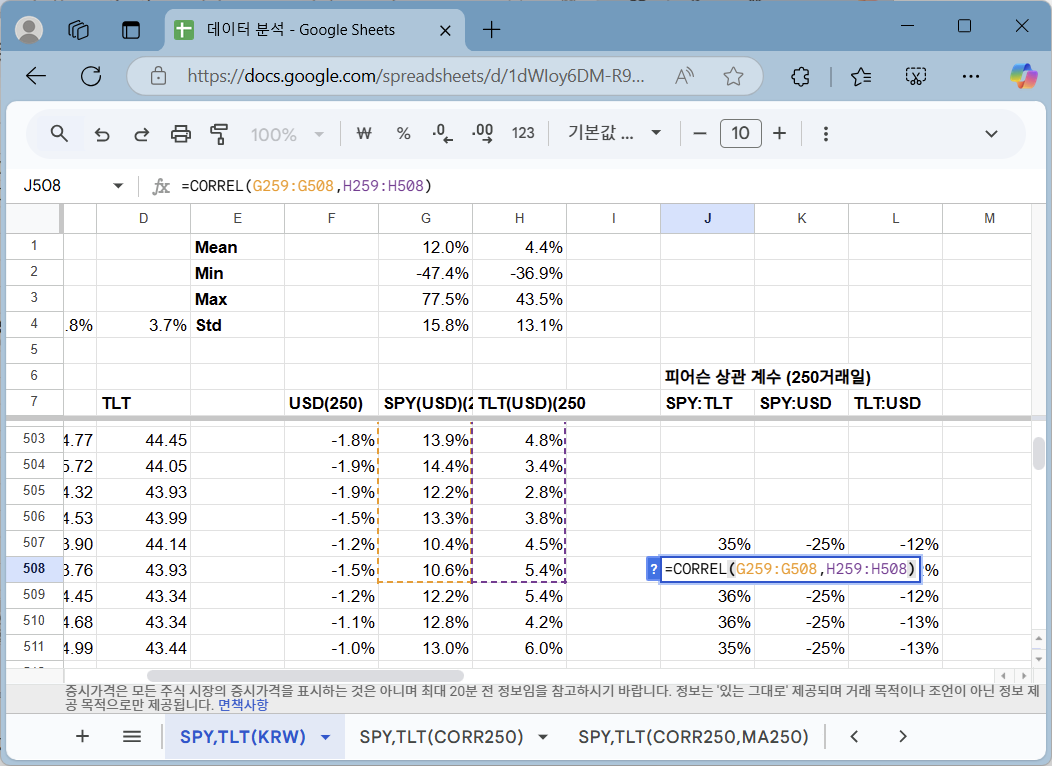
피어슨 상관계수 구하기 

다음 왼쪽 그림은 구글 시트로 환율, SPY, TLT의 1년(250거래일) 수익률을 계산한 것입니다.

자산별 1년 수익률과 1년 수익률 1년치를 이용한 피어슨 상관 계수 구하기

오른쪽 그림은 이렇게 계산한 1년 수익률 1년치(250거래일)에 대해 피어슨 상관 계수를 구한 것입니다. 계산한 피어슨 상관 계수를 그래프를 그려보면 다음과 같이 시간에 따라 어떻게 변했는지 볼 수 있습니다.

환율, SPY, TLT의 1년 수익률의 피어슨 상관 계수

각 점은 해당 시점에서 최근 1년간 두 자산 수익률의 상관성을 의미합니다. 피어슨 상관 계수는 +1에서 -1의 값을 가집니다. +1은 수익률의 방향이 동일하고, 상대 강도가 항상 일정했다는 의미입니다. 예를 들어 동일한 S&P 500 지수를 추종하는 SPY와 VOO 간에는 +1에 가까운 상관 계수가 계속 유지됩니다. 레버리지 ETF의 경우에도 기초자산과 방향은 동일하고, 상대 강도가 어느 정도 일정하기에 +1에 가까운 상관 계수가 나타납니다.

기초자산과 반대 방향으로 움직이는 인버스 ETF의 경우 상관 계수가 -1에 가까운 값이 됩니다. 현금과 같은 변동성이 없는 자산과의 상관 계수는 0이 되고, 금(gold)과 같이 주식과 특별한 관계가 없는 자산도 평균적으로 0에 가까운 상관 계수를 보일 수 있습니다.

상관 계수는 자산 간 혼합 시 얻을 수 있는 효과를 직접적으로 표현하는 지표는 아니지만, 혼합 포트폴리오의 대략적인 형태를 가늠하는데 도움이 됩니다. 두 자산을 혼합했을 때 만들어지는 포트폴리오의 최대 범위는 삼각형을 이루는데, 상관성에 따라 삼각형 내 어떤 모양의 선이 될지 어느 정도 결정되기 때문입니다. 참고: [초급 16] 서로 독립이면 혼합 포트폴리오는 어떤 형태가 될까? (독립이 아니면 어떻게 될까?)

여기서는 피어슨 상관 계수를 구할 때 1년 수익률을 사용했습니다. 환율 효과를 안정적으로 반영하고 한 번씩 계좌를 살펴보는 장기 투자자의 시각을 반영한 것입니다. 용도에 따라서는 일일 수익률 또는 5거래일 수익률을 이용하여 상관 계수를 계산하여 분석할 수도 있습니다.

생성된 그래프를 보면 조금 복잡합니다. 파란색의 SPY와 TLT 간에는 음의 상관성이 있는 듯하고, 빨간색인 SPY와 환율 간에도 음의 상관성이 보입니다. 노란색의 TLT와 환율은 양의 상관성을 보이기도 하고 음의 상관성을 보이기도 하는 듯 파악하기 어렵습니다.

이 연재에서 지금까지의 분석 방식은 정적 자산 배분을 염두에 두었습니다. 정적 자산 배분은 분석 대상 데이터의 모든 기간에 걸친 평균적인 자산 간 상관성을 이용합니다. 하지만 이 그래프에서 보듯, 자산 간 상관성은 일정하지 않고 상당히 큰 폭으로 계속 변합니다.

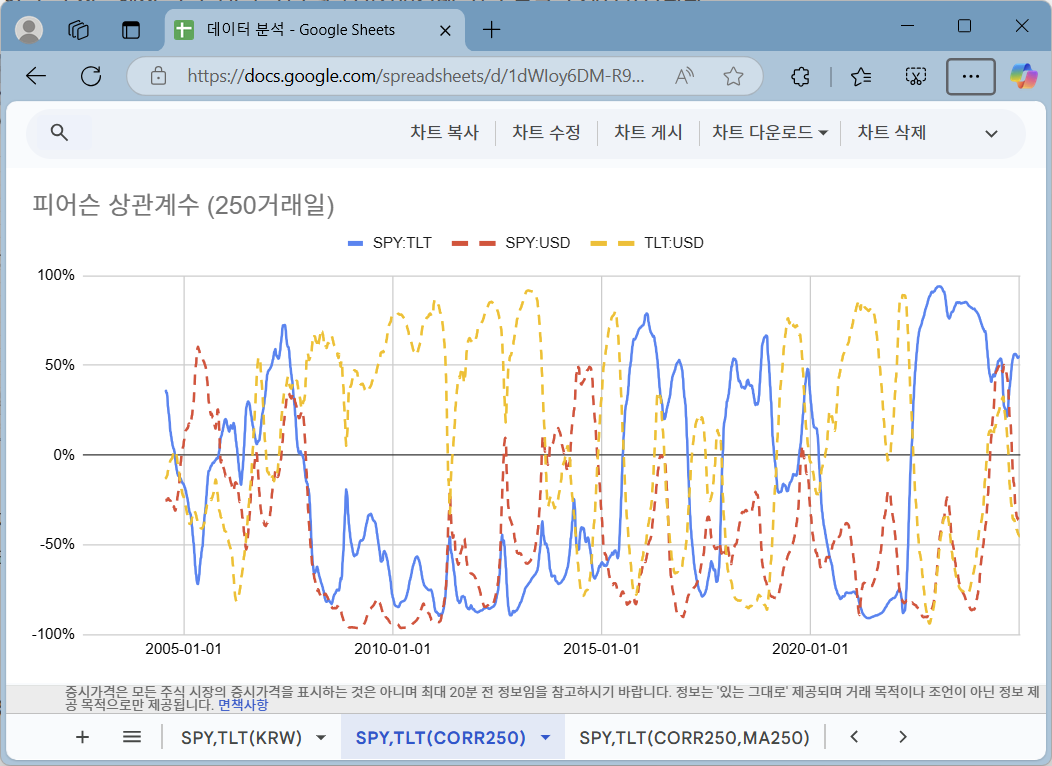
장기적인 자산 간 상관성 살펴보기 

상관 계수를 250거래일이 아닌 좀 더 긴 기간으로 계산하거나, 상관계수의 이동평균을 구하면 조금 더 일반적인 경향을 파악하기 유리합니다. 다음은 앞에서 계산한 상관 계수에 대해 250거래일 이동평균을 계산하고 이를 나타낸 그래프입니다. 참고: 이동평균을 다시 계산하는 것보다는 거래일 수를 늘리는 방법이 더 간편합니다.

상관 계수의 1년 이동평균

이제 자산 간 상관성이 조금 더 단순화되어 파악하기 쉽습니다. 오른쪽 그래프를 보면 파란색의 SPY와 TLT는 전반적으로 약한 음의 상관성을 가지고 있었습니다. 빨간색의 SPY와 환율은 꽤 강한 음의 상관성이 나타났습니다. 노란색의 TLT와 환율은 양의 상관성에 좀 더 가까웠습니다.

상관성을 시간의 흐름에 따른 변화 양상을 살펴보는 이유를 명확히 알고 있어야 합니다. 자산 간 상관성을 포함한 모든 통계량은 계속해서 변합니다. 그러니 투자자는 특정 통계량이 안정적인지, 아니면 어떤 요인에 의해 변화 가능성이 높은 것인지 파악해고 이를 고려해서 투자에 참고할 필요가 있습니다.

이 때문에 이 글에서 제시하는 방식처럼 다른 거래일수로 분석하기 위해 시트를 고쳐야 하는 방식은 효율적이지 않습니다. 거래일수와 같은 변수를 손쉽게 바꾸어가며 장기적인 통계량 변화와 중단기적인 통계량 변화를 모두 살펴보아야 하기 때문입니다. 동적으로 기간 수익률이나 이동평균을 재계산하기 위해서는 다음 편에서 소개하는 INDIRECT() 함수를 사용하면 됩니다. 참고: [데이터 분석 14] 두 자산의 수익률 분포를 비교해 보자 (구글 시트 편, feat. 미국배당다우존스 커버드콜)

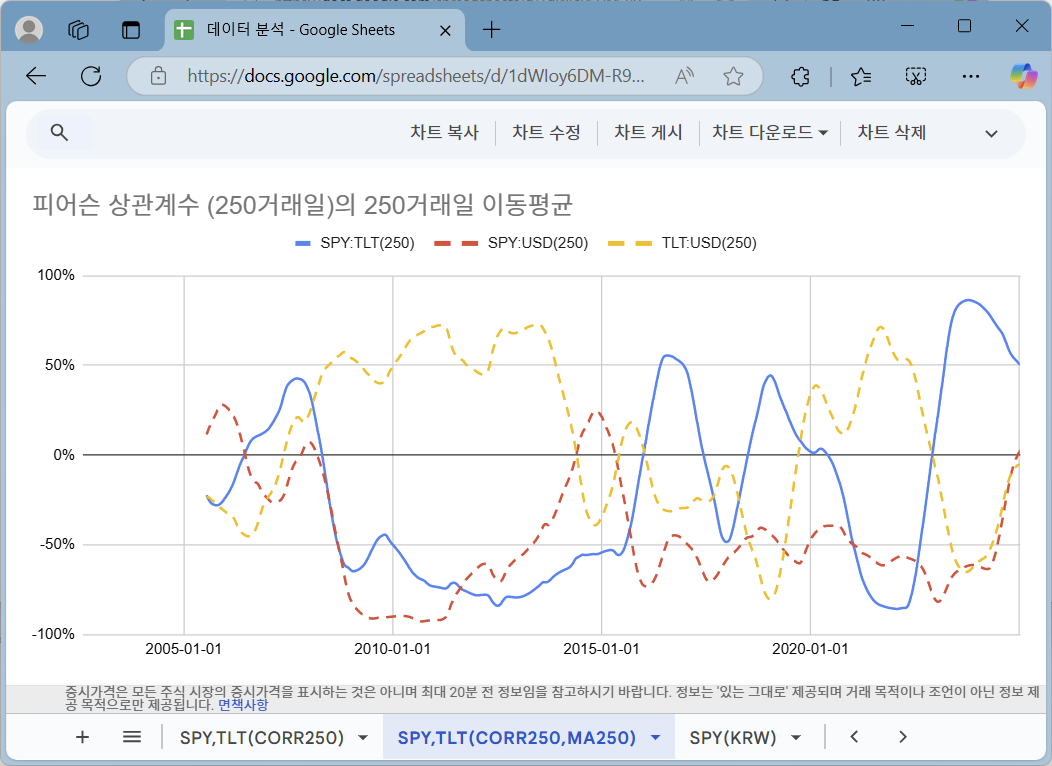
정리하며

이전까지 살펴보았던 분석은 모두 정적 분석이라 할 수 있습니다. 주어진 특정 기간의 데이터에 대한 평균적인 통계량을 산출하고 이를 이용하여 분석한 것입니다. 하지만 개별 자산에 대한 그리고 자산 간의 관계를 나타내는 통계량은 시간의 흐름에 따라 변할 수 있으며, 어떤 통계량은 상당히 큰 변동이 발생할 수 있습니다. 평균적으로 기대했던 투자 성과와는 단기적으로 상당히 다른 결과를 얻을 수 있다는 의미가 됩니다.

투자자는 통계량 변동 가능성을 감안하고, 변동 정도를 파악하여 자산 배분에 참고할 필요가 있습니다. 특히 통계량이 크게 변동한 적이 있었다면, 그 원인은 무엇이고 어떻게 대응하는 것이 적절할지 미리 고민해 볼 필요가 있습니다.

이어지는 글: [데이터 분석 13] 두 자산의 상대 수익률 변화를 살펴보자 (구글 시트 편)

목록: 자산 배분 분석 방법과 사례 글 모음 [목록] (순서대로 차근차근 읽기를 권합니다)

참고 서적: <왜 위험한 주식에 투자하라는 걸까? - 장기 투자와 분산 투자에 대한 통계학적 시각> - 이 연재에서 소개하는 각종 분석 방법의 의미를 소개합니다.

함께 읽으면 좋은 글:

• [데이터 분석 11] 환율을 고려해서 환노출 주가를 계산하고 평균-분산 그래프에서 환헤지와 비교해 보자 (구글 시트 편)
• [데이터 분석 10] 특정 포트폴리오를 평균-분산 그래프에 표시해 보자 (구글 시트 편)
• [데이터 분석 9] 세 자산의 혼합 포트폴리오를 평균-분산 그래프에 나타내 보자 (구글 시트 편)
• [데이터 분석 8] 두 자산의 혼합 포트폴리오를 평균-분산 그래프에 나타내 보자 (구글 시트 편)
• [데이터 분석 7] 자산과 예금의 혼합 포트폴리오를 평균-분산 그래프에 나타내 보자 (구글 시트 편)
• S&P 500 국내 ETF는 무엇이 좋을까? (국내 상장 ETF 9종 비교와 분석)
• 나스닥 100 국내 ETF는 무엇이 좋을까? (국내 상장 ETF 5종 비교와 분석)
• 한국인은 커버드콜 ETF에 장기 투자해도 좋을까? - 커버드콜 ETF에 대한 글 모음
• 당신이 커버드콜에 장기 투자하면 안되는 이유 (매년 100만원씩 손해보지 않는 방법) 출간에 부쳐 (샘플북 포함)
• QQQ5(QQQ 5배 레버리지)는 1년간 얼마나 녹았을까?